Магнитостатика. Векторный потенциал в магнитостатике. Потенциал магнитного диполя. Закон Био – Савара – Лапласса, страница 2

Используем формулу Стокса

                        .

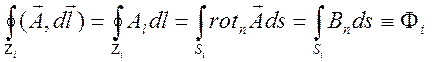Здесь  - поверхность, охватываемая контуром ;    - поток магнитной индукции через поверхность . В результате получаем искомое представление для магнитной энергии системы замкнутых токов

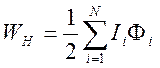                                    .                                            (8.11)

Это аналог формулы для энергии электростатического поя системы зарядов

                                    .

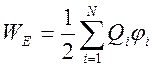Вследствии линейности уравнений, имеется линейная связь между полями  и  (это вектора с  компонентами, где  - число контуров):

                                                ,          ,

где  - матрица с элементами , называемыми коэффициентами взаимной индукции. Эти коэффициенты зависят только от геометрии контуров (зависят от формы, размеров, взаимного расположения) и не зависят от полей. Элементы  называются коэффициентами самоиндукции. Формула (8.11) представляется в виде

                                                .

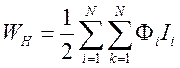Для одного контура стоком представление упрощается

                                                ,

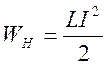где  - индуктивность этого контура.

            Найдем индуктивность элемента длины коаксиального кабеля. Поперечное сечение кабеля показано на Рис. 8.2. Пусть по внутреннему проводу радиуса  течет ток , а по внешнему проводу радиуса  течет ток обратного направления . Для энергии магнитного поля в элементе длины  коаксиального кабеля можно написать два представления:

1). 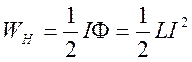                               ,                                                   (8.12)

2). 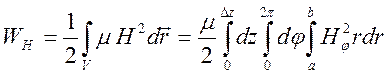                               .                  (8.13)

Для нахождения азимутальной составляющей  используем уравнение

:

,

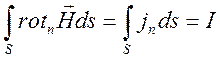где в качестве поверхности выбрана поверхность круга, перпендикулярного оси кабеля. Радиус этого круга . Используем формулу Стокса

                                    ,

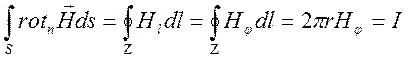найдем

                                                .

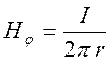Из формул (8.13) и (8.12) получим

                                                ,

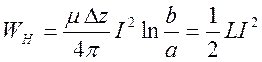что позволяет найти индуктивность элемента коаксиального кабеля

                                                .

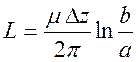8.3. Магнитостатика в материальных средах. Для описания магнитного поля в вакууме достаточно одного вектора  или , так как они связаны простым соотношением . В материальных средах. Намагниченность , магнитная индукция  и магнитное поле  связаны между собой линейным соотношением

.

Оно должно быть дополнено уравнениями материального состояния. В общем случае эти уравнения приводят к нелинейной зависимости . Вектор намагничивания  обусловлен наличием в среде молекулярных токов. Для большинства веществ магнитная индукция является линейной функцией напряженности поля вплоть до ее очень больших значений. Только для ферромагнетиков линейная зависимость наблюдается только при малой напряженности магнитного поля. и быстро сменяется нелинейной зависимостью. Для газов, жидкостей и поликристаллов различных веществ (исключая ферромагнетики) допустимо пользоваться линейной связью

                                                .

Для монокристаллов связь анизотропная: .

Вещества называются парамагнитными при , а при  вещества называются диамагнитными. В диамагнетиках при  нет собственных (спонтанных) магнитных моментов у атомов и молекул, т.е. орбитальные и спиновые магнитные моменты моменты уравновешены. При  в результате ларморовской прецесси электронных оболочек возникают магнитные моменты у атомов и молекул. Направления этих магнитных моментов противоположно магнитному полю. В паромагнетиках при  имеются собственные магнитные моменты у атомов и молекул. Собственный магнитный момент атома имеет двоякое происхождение: во – первых он возникает вследствие движения атомных электронов (орбитальный магнитный момент), и во – вторых, электрон обладает сам по себе собственным спиновым магнитным моментом. В паромагнетиках при  собственные магнитные моменты атомов распределены хаотически и суммарный момент равен нулю. При  в парамагнетиках наряду со слабым эффектом диамагнетизма, проявляется более заметный эффект упорядочения магнитных моментов атомов по внешнему полю. В результате магнитное поле внутри парамагнетика увеличивается. Парамагнитная восприимчивость убывает с ростом температуры. Эффект паромагнетизма аналогичен ориентационной поляризации в диэлектриках, помещенных в электрическое поле. Для диамагнетиков и парамагнетиков имеем представление для намагниченности

                                    ,

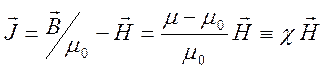     где  - магнитная восприимчивость,  у диамагнетиков и  у парамагнетиков. Потенциальная энергия  магнитного момента  имеет вид . Со стороны магнитного поля на магнитный момент действует сила

                        .

В случае ферромагнетиков атомы обладают собственными магнитными моментами, основную роль играют спиновые магнитные моменты определенных групп атомных электронов. Эти спиновые моменты в ничтожно слабом внешнем магнитном поле в подавляющем большинстве ориентированы по полю (этот эффект имеет квантовую природу). Этой их ориентации не препятствует тепловое движение при температуре ниже температуры Кюри. При более высокой температуре вещество становится парамагнетиком. В ферромагнетиках при  происходит сильное намагничивание вещества за счет больших внутренних магнитных моментов. При этом наблюдается нелинейная связь , имеет место гистерезис, который приводит к остаточному намагничиванию ферромагнетиков.