Геометрическая оптика. Учет влияния дифракционных эффектов

311. Геометрическая оптика. Учет влияния дифракционных эффектов.

Приближение геометрической оптики при распространении волн в неоднородной среде. Уравнения эйконала и переноса. Принцип Ферма. Точки поворота луча. Каустика. Лучевые трубки. Условия применимости приближения геометрической оптики. Описание лучевой картины для типичных случаев неоднородности. Оптико–механическая аналогия: взаимосвязь между принципами Ферма и Мопертюи. Постоянная Планка, длина волны де Бройля. Уравнение Шреденгера. Соотношение неопределенностей Гейзенберга. Радиус Бора. Принцип Гюйгенса и дифракция Френеля. Дифракция Фраунгофера.

11.1. Приближение геометрической оптики при распространении волн в неоднородной среде. Уравнения эйконала и переноса. Траектория луча. Принцип Ферма. Точка поворота луча. Геометрическое место точек поворота. Каустика. Лучевые трубки. Уравнение переноса. Уравнения Максвелла описывают все электромагнитные явления, в том числе и оптические. Однако, такой общий подход, как правило, очень сложен. При решении задач нужно учитывать граничные и начальные условия. Точные решения можно получить только в простейших случаях, когда задача характеризуется значительной симметрией. Имеется обширная область переменных полей, в которых уравнения Максвелла могут быть значительно упрощены. Это область очень коротких волн, когда длина волны в первом приближении вообще не фигурирует. Для этого нужно, чтобы длина волны  была значительно меньше всех характерных размеров  задачи. В этом случае распространение электромагнитного поля происходит вдоль геометрических линий, называемых лучами. Свойства этих лучей в первом приближении не зависят от длины волны. Законы электромагнитного поля формулируются на языке геометрии. Поэтому такая ситуация носит название геометрическая (или лучевая) оптика. Следующее приближение по малому параметру  учитывает волновую природу полей. Эти проявления носят общее название дифракционных явлений.

            1). Рассмотрим вопрос о распространении электромагнитных волн в неоднородной изотропной среде без пространственной дисперсии и без потерь. Ограничимся случаем гармонических полей. Задача сводится к решению уравнений Максвелла для комплексных амплитуд.

                                   

                                   

                                   

                                   

Уравнение для поля  получается из первых двух уравнений

                                   

Это уравнение перепишем в виде

                                   

Уравнение  дает представление для 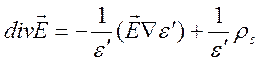. Ниже ограничимся такой поляризацией волны, что . Это позволяет получить уравнение для поля  в виде

                                    .

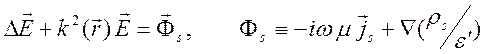Рассмотрим простейший вид неоднородности среды: . Согласно условию  рассматривается ситуация  (волна горизонтальной поляризации) . Поле вне источника описывается однородным скалярным уравнением

                                    .                      (11.1)

Представим волновое число в виде

                                    ,

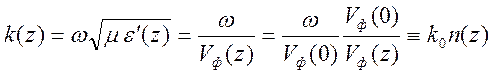где 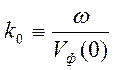 - волновое число на уровне  (выбор этого уровня произволен, он может выбираться, например, из соображений удобства написания формул), 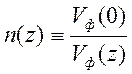 - показатель преломления неоднородной среды. Решение уравнения (11.1) будем искать в виде

                                                .                                           (11.1А)

Отметим, что это нелинейная замена неизвестной функции, и вместо одной неизвестной функции  введено две неизвестные функции  и . Это позволяет поставить дополнительное условие на новые неизвестные функции. Учитывая формулы дифференцирования

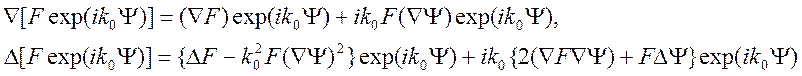
и принимая во внимание возможность постановки дополнительного условия, уравнение для  и  разобьем на систему двух нелинейных уравнений

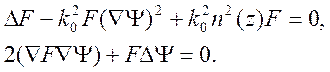                             (11.2)

            Второе уравнение системы (11.2) называется уравнением переноса. Благодаря нелинейной замене (11.1А), система уравнений (11.2) нелинейная.

В среде без потерь  и  - вещественные функции, при этом  - модуль функции , а  - это фаза функции . Ниже ограничимся рассмотрением именно такой ситуации (среда без потерь, или с очень малыми потерями). Функцию  называют оптическим путем или эйконалом («эйкон» - по – гречески «изображение», отсюда в русском языке слово «икона»). Если  - характерный пространственный масштаб изменения амплитуды поля  в среде, тогда справедливы оценки 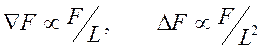. Учитывая это и требуя выполнения вышеотмеченного условия  или  (коротковолновое приближение), в первом уравнении системы (11.2) можно пренебречь слагаемым . В результате получим уравнение для  (уравнение эйконала), которое содержит только одну неизвестную функцию

                                                                                              (11.3)

После построения решения для эйконала  на основе (11.3), второе уравнение системы (11.2) используется для нахождения амплитудной функции .

Уравнение эйконала можно получить другим способом. Покажем как это можно сделать. По существу, представление  при условии, что  медленно изменяющаяся функция, является описанием квазимонохроматической волны. Поэтому можно ввести понятие локального волнового числа и на основе этого определения получить уравнение эйконала (11.3). В самом деле имеет место определение локального волнового числа