Будем
считать, что экран совпадает с нижней полуплоскостью ![]() (Рис.11.16),
так что ось
(Рис.11.16),
так что ось ![]() направлена по краю экрана. Ось
направлена по краю экрана. Ось ![]() ортогональна поверхности экрана и на этой
ортогональна поверхности экрана и на этой
оси
на расстоянии ![]() находится источник (слева от
начала координат). Координаты точки наблюдения равны
находится источник (слева от
начала координат). Координаты точки наблюдения равны ![]() .
Тогда координаты элемента
.
Тогда координаты элемента ![]() равны
равны ![]() и
и ![]() ,
,![]() . Наиболее существенны только близкие к
точке
. Наиболее существенны только близкие к
точке ![]() участки
участки ![]() ,
поэтому возможны упрощения на основе малости величин
,
поэтому возможны упрощения на основе малости величин ![]() по
сравнению с
по
сравнению с ![]()
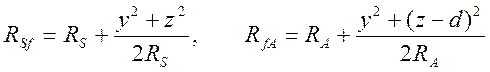 .
.
Учитывая,
что ![]() , получим
, получим
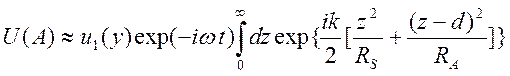 .
. 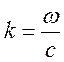 .
.
Верхний
предел интегрирования взят равным ![]() , так как область
больших
, так как область
больших ![]() не дает существенного вклада в результат
интегрирования. Воспользуемся представлением
не дает существенного вклада в результат
интегрирования. Воспользуемся представлением
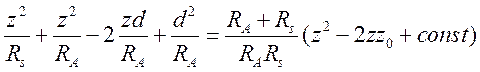 б
б
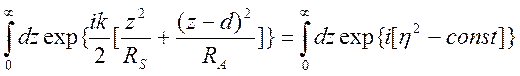 ,
,
где
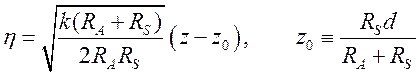 .
.
Результат преобразования имеет вид
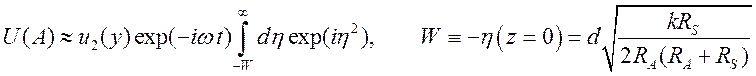 . (11.8)
. (11.8)
Последний
интеграл называется интегралом Френеля. Так как ![]() ,
то
,
то ![]() .
.
В случае ![]() точка наблюдения лежит
в области тени, интегрирование в (11.8) происходит в области выполнения
неравенства
точка наблюдения лежит
в области тени, интегрирование в (11.8) происходит в области выполнения
неравенства ![]() . Имеет место приближенная формула
. Имеет место приближенная формула
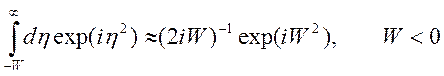 .
.
При ![]() точка наблюдения лежит
в освещенной области, интегрирование в (11.8) частично происходит в области,
где нарушается неравенство
точка наблюдения лежит
в освещенной области, интегрирование в (11.8) частично происходит в области,
где нарушается неравенство ![]() (это область в
окрестности
(это область в
окрестности ![]() ). Сделаем следующее преобразование
). Сделаем следующее преобразование 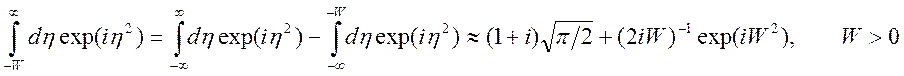 .
.
Квадрат
модуля интеграла Френеля определяет интенсивность ![]() электромагнитной
волны. График зависимости
электромагнитной
волны. График зависимости 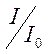 (
(![]() интенсивность вдали от экрана) изображен
на Рис.11.17. Вблизи экрана интенсивность в четыре раза меньше
интенсивность вдали от экрана) изображен
на Рис.11.17. Вблизи экрана интенсивность в четыре раза меньше ![]() . Если двигаться в освещенную область, то
интенсивность увеличивается и становится в максимуме порядка
. Если двигаться в освещенную область, то
интенсивность увеличивается и становится в максимуме порядка ![]() , далее начинаются осцилляции и приближение
интенсивности к значению
, далее начинаются осцилляции и приближение
интенсивности к значению ![]() .
.
11.16.
Дифракция Фраунгофера. Найдем теперь
поле дифрагировашей электромагнитной волны в случае, когда источник ![]() и точка наблюдения удалены на
бесконечность (Рис.11.18). Будем по-прежнему использовать принцип Гюйгенса,
взяв за поверхность
и точка наблюдения удалены на
бесконечность (Рис.11.18). Будем по-прежнему использовать принцип Гюйгенса,
взяв за поверхность ![]() плоскость, закрывающую
отверстие. Точка
плоскость, закрывающую
отверстие. Точка ![]() находящаяся на
находящаяся на ![]() будет началом координат, радиус вектор
будет началом координат, радиус вектор ![]() направлен из точки
направлен из точки ![]() в
элемент
в
элемент ![]() . Падающее поле в точке
. Падающее поле в точке ![]() поверхности
поверхности ![]() представим
в виде
представим
в виде ![]() . Точка наблюдения
. Точка наблюдения ![]() находится
далеко от отверстия экрана, поэтому направление дифрагирующего луча совпадает с
направлением радиус-вектора
находится
далеко от отверстия экрана, поэтому направление дифрагирующего луча совпадает с
направлением радиус-вектора ![]() этой точки. Волновой
вектор дифрагировавшего поля
этой точки. Волновой
вектор дифрагировавшего поля ![]() направлен по
направлен по ![]() .
. ![]() -
радиус вектор, направленный из элемента
-
радиус вектор, направленный из элемента ![]() в точку
наблюдения, причем
в точку
наблюдения, причем ![]() и
и 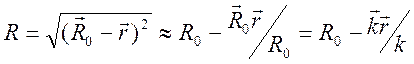 .
.
Следовательно,
![]() . На основе принципа Гюйгенса имеем поле в
точке наблюдения
. На основе принципа Гюйгенса имеем поле в
точке наблюдения
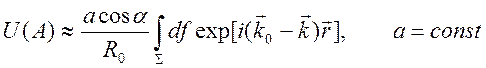 ,
,
![]() - угол падения луча на площадку
- угол падения луча на площадку ![]() ,
, ![]() .
.
В
отличие от дифракции Френеля, в которой был существенен вклад лишь небольшого
участка поверхности ![]() , при дифракции Фраунгофера
существенна вся эта поверхность.
, при дифракции Фраунгофера
существенна вся эта поверхность.
В
качестве примера рассмотрим дифракцию на бесконечно длинной щели с
параллельными границами в непрозрачном экране (Рис.11.19). Пусть волновой
вектор падающей волны![]() ортогонален к плоскости экрана
ортогонален к плоскости экрана ![]() . Угол дифракции
. Угол дифракции ![]() -
это угол между векторами
-
это угол между векторами ![]() и
и ![]() . Ширина щели
. Ширина щели ![]() ,
поэтому имеем
,
поэтому имеем
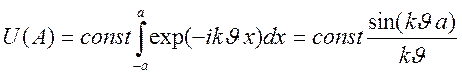 ,
,
где
учтено, что ![]() ,
, ![]() .
Интенсивность дифрагировавшей в интервал углов
.
Интенсивность дифрагировавшей в интервал углов ![]() волны
пропорциональна
волны
пропорциональна ![]() :
:
![]() .
.
Найдем коэффициент пропорциональности, используя представление для суммарной интенсивности волны, падающей на щель
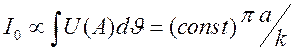 .
.
Зависимость
интенсивности дифрагировавшего луча от угла дифракции показана на Рис.11.20,
где введено обозначение ![]() . Интенсивность имеет
ряд быстро убывающих максимумов, разделенных минимумами при
. Интенсивность имеет
ряд быстро убывающих максимумов, разделенных минимумами при 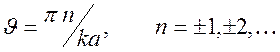 , в которых она обращается в нуль.
Установив положение минимумов (или максимумов) можно определит длину волны.
Точность такого определения длины волны по дифракции на одной щели невелика
из-за слабой резкости. Точность можно повысить, используя дифракционную
решетку (совокупность одинаковых параллельных щелей, расположенных на
равном расстоянии друг от друга).
, в которых она обращается в нуль.
Установив положение минимумов (или максимумов) можно определит длину волны.
Точность такого определения длины волны по дифракции на одной щели невелика
из-за слабой резкости. Точность можно повысить, используя дифракционную
решетку (совокупность одинаковых параллельных щелей, расположенных на
равном расстоянии друг от друга).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.