(1) ![]() - минимальный размер атома (радиус Бора)
- минимальный размер атома (радиус Бора)
(2) ![]() , здесь
, здесь ![]() - масса
и кинетическая энергия электрона
- масса
и кинетическая энергия электрона
(3) 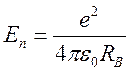 - потенциальная энергия электрона
- потенциальная энергия электрона
(4) ![]() .
.
Из этих соотношений получается представление радиуса Бора
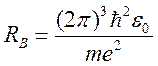 .
.
Возможно
обобщение классической квантовой механии на случай релятивистской квантовой
механики при введении биспинора (четыре волновых функции), который
удовлетворяет уравнению Дирака. Система уравнений Дирака совместно с
уравнениями Максвелла описывают квантовую электродинамику. В этом описании
возникают эффекты: 1). Электрон обладает внутренним моментом количества
движения – спином (он равен ![]() в единицах квантовой
постоянной). 2). Электроны могут иметь состояния с отрицательной энергией
(бесконечный фон электронов составляет электронный вакуум). Такое
состояние соответствует наличию позитронов – это античастицы по отношению к
электронам. Позитроны имеют массу электрона и их заряд отличается от заряда
электрона только знаком. Электромагнитное поле и электроны с позитронами
выступают в квантовой электродинамике как две равноценные формы единой материи.
в единицах квантовой
постоянной). 2). Электроны могут иметь состояния с отрицательной энергией
(бесконечный фон электронов составляет электронный вакуум). Такое
состояние соответствует наличию позитронов – это античастицы по отношению к
электронам. Позитроны имеют массу электрона и их заряд отличается от заряда
электрона только знаком. Электромагнитное поле и электроны с позитронами
выступают в квантовой электродинамике как две равноценные формы единой материи.
11.5.
Принцип Гюйгенса и дифракция Френеля. Геометрическая
оптика соответствует коротковолновому приближению для электромагнитных волновых
процессов (длина волны ![]() ). При конечных значениях длины
волны возникают отличия от геометрической оптики, – они носят общее название дифракции.
). При конечных значениях длины
волны возникают отличия от геометрической оптики, – они носят общее название дифракции.
1). Дифракционные
явления при малых ![]() можно исследовать на основе
использования принципа Гюйгенса (речь будет идти о поправках к
геометрической оптике). Рассмотрим следующую задачу. На пути
распространения электромагнитного поля от источника
можно исследовать на основе
использования принципа Гюйгенса (речь будет идти о поправках к
геометрической оптике). Рассмотрим следующую задачу. На пути
распространения электромагнитного поля от источника ![]() к точке
наблюдения
к точке
наблюдения ![]() находится непрозрачный экран с отверстием
(Рис.11.5). Считается, что волна распространяется в вакууме. Принцип Гюйгенса
предлагает считать отверстие закрытым произвольной поверхностью
находится непрозрачный экран с отверстием
(Рис.11.5). Считается, что волна распространяется в вакууме. Принцип Гюйгенса
предлагает считать отверстие закрытым произвольной поверхностью ![]() , которая является источником вторичных
волн, распространяющихся за экран (в частности в точку
, которая является источником вторичных
волн, распространяющихся за экран (в частности в точку ![]() ).
При этом считается, что источник
).
При этом считается, что источник ![]() сам непосредственно не
создает поле в точке
сам непосредственно не
создает поле в точке ![]() . Источник
. Источник ![]() создает только вторичные источники на
поверхности
создает только вторичные источники на
поверхности ![]() . Этими вторичными источниками являются
элементы
. Этими вторичными источниками являются
элементы ![]() поверхности
поверхности ![]() .
Монохроматическое поле, создаваемое на элементе
.
Монохроматическое поле, создаваемое на элементе ![]() равно
равно 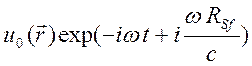 , где
, где ![]() -
расстояние от источника до элемента
-
расстояние от источника до элемента ![]() . Это поле
пропорционально
. Это поле
пропорционально ![]() , где
, где ![]() - угол
между нормалью
- угол
между нормалью ![]() к элементу
к элементу ![]() и направлением луча, падающего на площадку
и направлением луча, падающего на площадку
![]() . Это поле создается источником
. Это поле создается источником ![]() на элементе
на элементе ![]() в том
случае, если бы никакого экрана не было. Элемент
в том
случае, если бы никакого экрана не было. Элемент ![]() создает
за экраном сферическую волну, амплитуда которой убывает по закону
создает
за экраном сферическую волну, амплитуда которой убывает по закону ![]() , где
, где ![]() -
расстояние от элемента
-
расстояние от элемента ![]() до точки наблюдения
до точки наблюдения ![]() . При распространении сферической волны
нужно учесть эффект запаздывания ее. Для этого при нахождении поля в точке
. При распространении сферической волны
нужно учесть эффект запаздывания ее. Для этого при нахождении поля в точке ![]() в момент времени
в момент времени ![]() ,
нужно взять поле на элементе
,
нужно взять поле на элементе ![]() в боле ранний момент
времени
в боле ранний момент
времени ![]() Поле, создаваемое
Поле, создаваемое ![]() в
точке
в
точке ![]() , представляется в виде
, представляется в виде
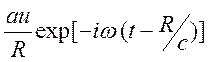 , где
, где ![]() .
.
Математическая формулировка принципа Гюйгенса заключается в следующем: результирующе поле находится в виде суперпозиции
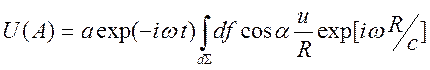 .
.
Ниже
рассмотрим два простейших дифракционных явления: дифракция Френеля (расстояние
между ![]() и
и ![]() конечно)
и дифракция Фраунгофера (
конечно)
и дифракция Фраунгофера (![]() и
и ![]() находятся на бесконечности).
находятся на бесконечности).
2).
При рассмотрении дифракции Френеля будем интересоваться поправками к
геометро-оптическому приближению. Поэтому учтем вклад только участков
поверхности ![]() , примыкающим к ломаной прямой, соединяющей
, примыкающим к ломаной прямой, соединяющей
![]() и
и ![]() .
Соответствующий участок края экрана будем считать прямолинейным. Амплитуда поля
изменяется медленно по сравнению с изменением фазы, поэтому
.
Соответствующий участок края экрана будем считать прямолинейным. Амплитуда поля
изменяется медленно по сравнению с изменением фазы, поэтому
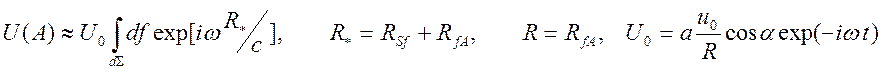
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.