11.4.
Оптико–механическая аналогия: взаимосвязь между принципами Ферма и Мопертюи.
Постоянная Планка, длина волны де Бройля. Уравнение Шреденгера. Соотношение
неопределенностей Гейзенберга. Радиус Бора Луч в геометрической оптике подобен траектории материальной частицы в
механике. Существует аналогия между принципом Ферма в геометрической оптике и
принципом Мопертюи в механике. Принцип Ферма утверждает минимальность
оптического пути высокочастотного электромагнитного поля (света). Интеграл,
взятый вдоль луча между двумя точками минимален по сравнению с оптическим
путем, вычисленным вдоль любой другой кривой, соединяющей те же точки ![]() и 2:
и 2:
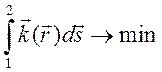 ,
,
где
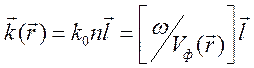 - волновой вектор,
- волновой вектор, ![]() -
частота волны,
-
частота волны, 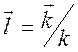 , волновой вектор направлен по
касательной к лучу.
, волновой вектор направлен по
касательной к лучу.
Принцип Мопертюи утверждает минимальность интеграла действия
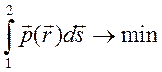 ,
,
взятого вдоль истинной траектории частицы, по сравнению с таким же интегралом, взятом вдоль любой другой кривой, соединяющей те же две точки.
Уравнение движения частицы в потенциальном поле в нерелятивистском случае имеет вид
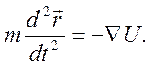
Здесь
![]() - масса частицы,
- масса частицы, ![]() -
потенциальная энергия.
-
потенциальная энергия.
Так
как 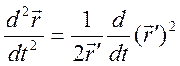 (здесь штрихом обозначена производная по
времени), то из уравнения движения следует закон сохранения энергии
(здесь штрихом обозначена производная по
времени), то из уравнения движения следует закон сохранения энергии
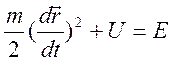 ,
,
или
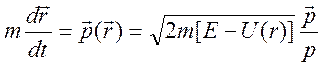 .
.
![]() - импульс частицы, он направлен по
касательной к траектории частицы,
- импульс частицы, он направлен по
касательной к траектории частицы, ![]() - энергия частицы.
- энергия частицы.
Имеет место аналогия ![]() .
Аналогом материальной точки в механике является волновой пакет в геометрической
оптике. Должна иметься аналогия
.
Аналогом материальной точки в механике является волновой пакет в геометрической
оптике. Должна иметься аналогия ![]() (
(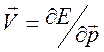 - скорость частицы),
- скорость частицы), 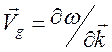 . Отсюда следует аналогия
. Отсюда следует аналогия ![]() . Количественная формулировка
оптико-механической аналогии выглядит следующим образом
. Количественная формулировка
оптико-механической аналогии выглядит следующим образом
![]() ,
,
где
![]() - постоянная Планка. В частности
имеем
- постоянная Планка. В частности
имеем 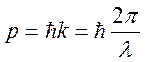 или
или 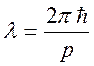 - длина
волны де Бройля. Фазовая скорость имеет представление
- длина
волны де Бройля. Фазовая скорость имеет представление 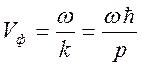 . Волновому уравнению в электродинамике
сопоставим аналогичное волновое уравнение для механики
. Волновому уравнению в электродинамике
сопоставим аналогичное волновое уравнение для механики
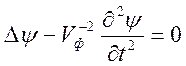 ,
,
где
![]() - волновая функция, описывающая
монохроматическую волну
- волновая функция, описывающая
монохроматическую волну ![]() , для которой волновое
уравнение приводится к виду уравнения с переменным коэффициентом
, для которой волновое
уравнение приводится к виду уравнения с переменным коэффициентом ![]() :
:
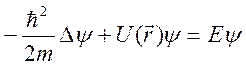 .
.
Это
уравнение Шреденгера для комплексной амплитуды волновой функции в
квантовой механике. Величина ![]() описывает распределение
вероятностей нахождения частицы в том или ином месте пространства. Возникает
вопрос, почему имеет место квантование? Это обусловлено тем, что при заданной
потенциальной энергии
описывает распределение
вероятностей нахождения частицы в том или ином месте пространства. Возникает
вопрос, почему имеет место квантование? Это обусловлено тем, что при заданной
потенциальной энергии ![]() уравнение Шредингера допускает
решение не при всех, а только при определенных значениях энергии
уравнение Шредингера допускает
решение не при всех, а только при определенных значениях энергии ![]() . Этот набор энергий называется спектром
энергий. Спектр может быть дискретным (наличие квантования) и может быть
сплошным. Если в качестве примера взять
. Этот набор энергий называется спектром
энергий. Спектр может быть дискретным (наличие квантования) и может быть
сплошным. Если в качестве примера взять ![]() (это
соответствует потенциальной энергии электрона в поле протона), то можно
получить энергетический спектр атома водорода.
(это
соответствует потенциальной энергии электрона в поле протона), то можно
получить энергетический спектр атома водорода.
Для волнового пакета (квазимонохромата) имели место соотношения
![]() .
.
Аналогами их в квантовой механике будут соотношения неопределенности Гейзенберга
![]() .
.
Если
частица локализована в интервале ![]() по оси
по оси ![]() , то проекция ее импульса на эту ось не
может иметь определенного значения, а лежит в интервале
, то проекция ее импульса на эту ось не
может иметь определенного значения, а лежит в интервале ![]() при
выполнении условия
при
выполнении условия ![]() (аналогично для осей
(аналогично для осей ![]() и
и ![]() ). Если
частица нестационарна в течение времени
). Если
частица нестационарна в течение времени ![]() , то это
состояние не может быть моноэнергетическим. Мера немоноэнергетичности
, то это
состояние не может быть моноэнергетическим. Мера немоноэнергетичности ![]() связана с
связана с ![]() соотношением
Гейзенберга.
соотношением
Гейзенберга.
Оценку
величины радиуса самого легкого атома – атома водорода можно получить на основе
предельной ситуации, заменяя неравенство Гейзенберга равенством ![]() , сделав дополнительно четыре допущения:
, сделав дополнительно четыре допущения:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.