![]() (11.4)
(11.4)
где
![]() , и
, и 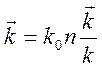 . В
результате из определения (11.4) получается уравнение эйконала (11.3).
. В
результате из определения (11.4) получается уравнение эйконала (11.3).
Поверхности равной фазы ![]() носят название волновых поверхностей. Будем
искать решение уравнения эйконала (11.3) в виде суммы трех функций, каждая из
которых зависит только от одной координаты
носят название волновых поверхностей. Будем
искать решение уравнения эйконала (11.3) в виде суммы трех функций, каждая из
которых зависит только от одной координаты
![]() .
.
При этом уравнение эйконала принимает вид
![]()
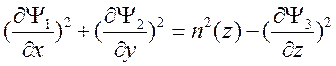 .
.
В левой части этого уравнения стоят функции не зависящие от ![]() , а в правой части функции зависят от
, а в правой части функции зависят от ![]() . Это может быть только в том случае, когда
эти функции являются постоянными величинами.
. Это может быть только в том случае, когда
эти функции являются постоянными величинами.
Ведя обозначения 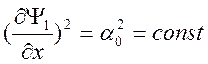 ,
, 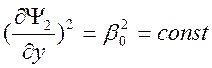 , получим решение в виде
, получим решение в виде
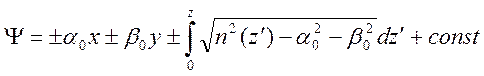 .
.
Значение ![]() соответствует точке внутри
источника. Для нахождения входящих в это выражение постоянных величин
воспользуемся тем, что в малой окрестности источника среду можно считать
однородной
соответствует точке внутри
источника. Для нахождения входящих в это выражение постоянных величин
воспользуемся тем, что в малой окрестности источника среду можно считать
однородной ![]() . Здесь эйконал должен совпадать с
эйконалом плоской волны, распространяющейся в направлении волнового вектора
. Здесь эйконал должен совпадать с
эйконалом плоской волны, распространяющейся в направлении волнового вектора
![]() ,
,
где ![]() - направляющие косинусы вектора
- направляющие косинусы вектора ![]() . Для волны, распространяющейся в сторону
увеличения значений координат, имеем
. Для волны, распространяющейся в сторону
увеличения значений координат, имеем
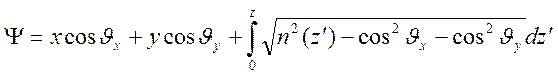 .
.
Вращением системы координат вокруг оси ![]() можно
добиться того, что
можно
добиться того, что ![]() . Вместо угла
. Вместо угла ![]() введем в рассмотрение угол выхода волны
(луча) (Рис.11.1)
введем в рассмотрение угол выхода волны
(луча) (Рис.11.1) ![]() и получим
и получим
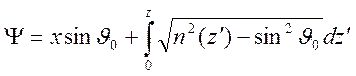 . (11.5)
. (11.5)
Введем единичный вектор 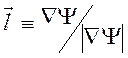 , ортогональный
поверхностям равной фазы
, ортогональный
поверхностям равной фазы ![]() . В среде без потерь
согласно уравнению эйконала (11.3) имеем представление
. В среде без потерь
согласно уравнению эйконала (11.3) имеем представление ![]() .
Линия, в каждой точке которой вектор
.
Линия, в каждой точке которой вектор ![]() касателен, называется лучом.
Существует другое определение луча: луч это геометрическое место точек с
максимальным значением поля. Без доказательства отметим, что в изотропной среде
оба определения эквивалентны. В случае анизотропных сред эти два определения
дают различные лини (траектории). В каждой точке луча в изотропной среде имеем
касателен, называется лучом.
Существует другое определение луча: луч это геометрическое место точек с
максимальным значением поля. Без доказательства отметим, что в изотропной среде
оба определения эквивалентны. В случае анизотропных сред эти два определения
дают различные лини (траектории). В каждой точке луча в изотропной среде имеем
![]() ,
,
где ![]() - угол между лучом и осью
- угол между лучом и осью ![]() в данной точке луча.
в данной точке луча.
С другой стороны, при учете (11.5) имеем представление для среды без потерь
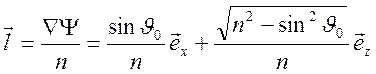 .
.
Значит, справедливы формулы, дающие закон Снеллиуса для неоднородной среды
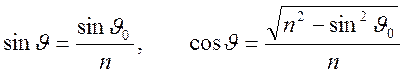 .
.
2). Получим уравнение, описывающее траекторию луча, для
этого выделим элемент ![]() этой траектории. Так как
этой траектории. Так как ![]() , то имеет место
, то имеет место
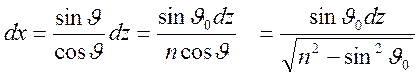 .
.
Интегрируя это соотношение, получим уравнение, описывающее траекторию луча
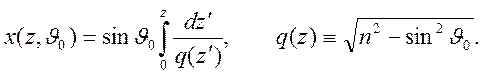
Уравнение луча может использоваться для различных целей.
1.
Оно пригодно для
построения зависимости ![]() при заданном значении угла
выхода луча
при заданном значении угла
выхода луча ![]() .
.
2.
По заданным
координатам точек наблюдения и источника, можно найти угол выхода луча ![]() . В этой задаче находится такой угол выхода
луча
. В этой задаче находится такой угол выхода
луча ![]() , при котором луч «выйдя» из источника
попадет в точку наблюдения. Следует отметить , что эта задача может иметь
несколько решений: в точку наблюдения может попадать несколько лучей от одного
источника.
, при котором луч «выйдя» из источника
попадет в точку наблюдения. Следует отметить , что эта задача может иметь
несколько решений: в точку наблюдения может попадать несколько лучей от одного
источника.
При распространении волны в неоднородной среде происходит
«искривление» луча. Возможен «поворот» луча. Точкой поворота луча в
среде с зависимостью ![]() , называется наивысшая точка на
траектории луча (Рис.11.2). В этой точке угол выхода луча становится прямым
, называется наивысшая точка на
траектории луча (Рис.11.2). В этой точке угол выхода луча становится прямым ![]() , поэтому
, поэтому ![]() .
Соотношение
.
Соотношение ![]() можно использовать для нахождения высоты
точки поворота луча , вышедшего из источника под углом
можно использовать для нахождения высоты
точки поворота луча , вышедшего из источника под углом ![]() .
Горизонтальная координата точки поворота определяется интегралом
.
Горизонтальная координата точки поворота определяется интегралом
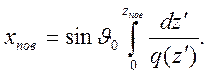
Геометро - оптическое приближение поля имеет вид
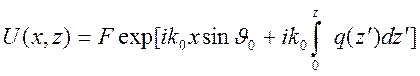 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.