где эконал ![]() считаем уже найденным.
Выделим участок лучевой трубки, ограниченный с торцов элементами площади
считаем уже найденным.
Выделим участок лучевой трубки, ограниченный с торцов элементами площади ![]() и
и![]() ,
перпендикулярными лучам в трубке, и следовательно совпадающими с поверхностями
равной фазы (Рис.11.4). Введем вспомогательный вектор
,
перпендикулярными лучам в трубке, и следовательно совпадающими с поверхностями
равной фазы (Рис.11.4). Введем вспомогательный вектор ![]() (рассматривается
среда без потерь). Имеет место
(рассматривается
среда без потерь). Имеет место
![]() .
.
Следствием является
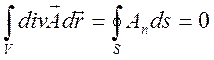 ,
,
где ![]() - объем выделенного участка
лучевой трубки,
- объем выделенного участка
лучевой трубки, ![]() - поверхность, ограничивающая
этот объем. Так как вектор
- поверхность, ограничивающая
этот объем. Так как вектор ![]() ориентирован вдоль
луча, то имеем
ориентирован вдоль
луча, то имеем
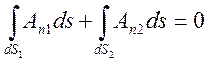 ,
,
из которого для короткой трубки, у которой ![]() ,
получаем
,
получаем ![]() или
или ![]() . В
лучевой трубке справедливо представление для амплитудного множителя
. В
лучевой трубке справедливо представление для амплитудного множителя
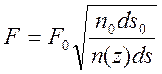 . (11.6)
. (11.6)
Так как ![]()
![]() , то
при
, то
при ![]() (это происходит в окрестности каустики),
имеет место резкое изменение функции
(это происходит в окрестности каустики),
имеет место резкое изменение функции ![]() .
.
11.2. Условия применимости приближения геометрической оптики. В более общем случае, решение уравнения (11.1) можно построить в виде
![]() ,
,
где
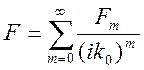 .
.
Подставляя
эти выражения в уравнение (11.1), и приравнивая нулю коэффициенты при
одинаковых степенях ![]() , в нулевом приближении получим
уравнение эйконала
, в нулевом приближении получим
уравнение эйконала
![]() ,
,
а
в следующих приближениях возникает система рекуррентных уравнений для амплитуд ![]()
![]() ,
,
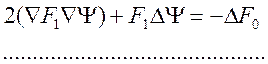
Приближению геометрической оптики соответствует представление
![]() .
.
Основное
условие применимости такого приближения связано с пренебрежением в равнении
(11.2)слагаемым ![]() . Это условие можно записать в
виде
. Это условие можно записать в
виде
![]() . (11.7)
. (11.7)
Используем
приближенное представление (11.6) 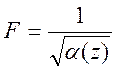 (
(![]() )для медленно изменяющейся амплитуды и
получим ограничения на свойства среды и частоту. Произведем оценки
)для медленно изменяющейся амплитуды и
получим ограничения на свойства среды и частоту. Произведем оценки
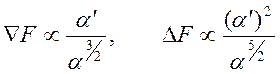 ,
,
условие (11.7) принимает вид
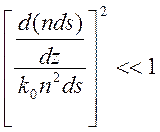 , или
, или 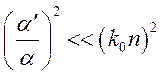 .
.
Это
условие нарушается там, где ![]() (в окрестности
каустики) и нарушение происходит при
(в окрестности
каустики) и нарушение происходит при ![]() . Приближение геометрической
оптики нарушается в области, где функция
. Приближение геометрической
оптики нарушается в области, где функция ![]() изменяется
резко.
изменяется
резко.
11.3. Описание лучевой картины для типичных случаев неоднородности.
1). Рассмотрим задачу о картине лучей в неоднородной безграничной среде, квадрат показателя преломления которой изменяется с высотой по линейному закону
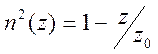 .
.
Уравнение луча в такой среде принимает вид
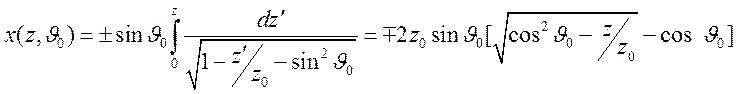 .
.
Таким
образом, лучи ![]() являются параболами. Для луча,
идущего в сторону увеличения координат
являются параболами. Для луча,
идущего в сторону увеличения координат ![]() и
и ![]() , следует брать верхний знак Высота точки
поворота находится из условия
, следует брать верхний знак Высота точки
поворота находится из условия ![]() и выражается формулой
и выражается формулой
![]() .
.
Уравнение луча приводится к виду
![]() .
.
Горизонтальная координата точки поворота дается формулой
![]() .
.
Найдем
горизонтальную координату («дальность») луча, пришедшего на тот же уровень, с
которого он и вышел (![]() ) (Рис.11.5)
) (Рис.11.5)
![]() .
.
Одной
дальности соответствует два луча, вышедшие из источника под углами ![]() и
и ![]() (Рис.
11.6). Таким образом, в одну точу
(Рис.
11.6). Таким образом, в одну точу ![]() , на уровне
, на уровне ![]() приходят два луча (при условии
приходят два луча (при условии ![]() ). Это соответствует отмеченной выше
ситуации, когда задача нахождения угла выхода при фиксированных положениях
источника и точки наблюдения, имеет не единственное решение.
). Это соответствует отмеченной выше
ситуации, когда задача нахождения угла выхода при фиксированных положениях
источника и точки наблюдения, имеет не единственное решение.
Найдем геометрическое место точек поворота. Оно определяется системой уравнений
![]() ,
,
из которой получаем
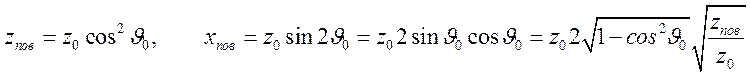 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.