Проектировочный расчет двухступенчатого планетарного редуктора, страница 5

2.7.10. Величина коэффициента неравномерности распределения нагрузки по ширине венцов и среди сателлитов.

k_FS = W + (k^o_Fb - 1) k_FW = 1,03 + (1,15 - 1) * 1 = 1,18

2.7.11. Делительный диаметр шестерни (солнечного колеса), мм.

(d)’_aF = (2 * 103 * T_F1 * z_a * k_FV * k_FS * U_F / (y_bd)₁ * [s_F])^1/3 = 57,3 мм

2.7.12. Предварительное значение модуля.

m’ = (d)’_aF / z_a = 57,3 / 17 = 3,37. Принимаем m = 3,5 мм.

2.7.13.Проверочный расчет.

Так как (d_W)’_ан = 65,21, что больше (d)’_aF = 57,3 мм, то производим корректировку чисел зубьев колес:

z_a = (d_W)’_ан / m = 65,21 / 3,5 = 18,6. Назначаем z_a = 19, тогда A = 19 (1 + 3,6) / 3 = 29,1. Округляем до ближайшего целого четного числа N = 30.                         z_b = 30 * 3 – 19 = 71;             z_g = (71 – 19) / 2 = 26; p_факт = 71/19 = 3,73;                  D% = (3,6 – 3,73) / 3,6 = 0,038 = 3,8 % < 5 %.

2.7.14. Скорректированная ширина венцов.

Так как (d_W)’_ан > (d)’_aF, то b_W = 716³ * T_H1 * k_HS * k_HV * (u + 1) / (d_a)² * u * [s_H]² = 716³ * 253,3 * 1,18 * 1,1 * ((26/19) + 1) / 66,5² * (26/19) * (1092,5)² = 39,57 мм. Принимаем b_W = 40 мм. Уточнение относительной ширины зубчатого венца солнечного колеса: (y_bd)_a = b_W / d_a = 40 / 66,5 = 0,6.

2.7.15. Таблица окончательных данных.

za = 19	UFa = 4,1	[sF]a = 470,6 Мпа	UFg / [sF]a = 0,87 * 10-2	da = 66,5
zg = 26	UFg = 3,8	[sF]b = 353 Мпа	UFg / [sF]g = 1,07 * 10-2	dg = 91
zb = 71	UFb = 3,6			db = 248,5
p = 3,73	m = 3,5 мм	bW = 40 мм	(ybd)a = 0,6

2.7.16. Обоснование выбора марки стали и ее термообработки для колеса b.

Величина контактных напряжений в зацеплении ‘g – b’

[s_H]_g-b = [s_H]_a-g / p^0,5 = 1092,5 / 3,73^0,5 = 566 Мпа.

Требуемая для этого уровня напряжений твердость поверхностей зубьев колеса в HB:

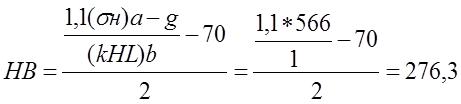Действующие максимальные напряжения в зубьях колеса b, МПа:

(s_F)_b = 2 * 103 * T_F1 * k_FS * k_FV * U_Fb / b_W * (d)_a * m = 258,9.

Необходимые для этого уровня напряжений твердость сердцевины зубьев, HB:

Для центрального колеса b выбираем сталь 40Х ГОСТ 4543 – 75, термообработка – улучшение до HB (270 – 300).

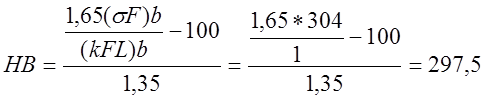2.8.      Определение зубчатых колес планетарного редуктора из условия работоспособности подшипников сателлита. Проектирование узла сателлита.

2.8.1.   Быстроходная ступень.

Исходные данные.

Наименование параметра	Условное обозначение	Величина	Размерность
Max. момент на центральном колесе	Та	134	Н * м
Коэф-т неравномерности нагрузки между сателлитами	W	1,03	-
Число сателлитов	nW	3	-
Модуль	m	2,0	мм
Параметр планетарной ступени	p	4,7	-
Число зубьев: центрального колеса b центрального колеса a сателлита g	zb za zg	34 20 37	- - -
Делительный диаметр центрального колеса a, удовлетворяющий изгибной прочности	(d)AF	32,2	мм
Диаметр начальной окружности центрального колеса а, удовлетворяющий контактной выносливости	(dW)aн	40,2	мм
Коэффициент формы зуба колеса, лимитирующего изгибную выносливость	YF	3,85	-
Эквивалентное число  циклов перемен напряжений сателлита при расчете контактной выносливости	NHEg	130 * 106	-
Частота вращения сателлита	(ng - nh)	643	об / мин
Рабочая ширина зубчатого венца	bW	17	мм

·  Определяем минимальный диаметр сателлита, обеспечивающий работоспособность встроенного подшипника. При расчете принимаем эквивалентное число миллионов оборотов подшипника

L @ N_HEg * 10^-6 = 130 млн.об.

(d_W)’_gnk = 8,2 * (T_a * W * (p - 1) * L_E^0,3 / n_W)^1/3 = 8,2 * (134 * 1,03 * (4,7 - 1) * 130^0,3 / 3) = 79 мм.