Асинхронный электропривод механизма подъема перегрузочного крана, страница 3

Откуда:

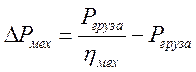
Подставляя в уравнение (6) получим:

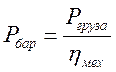
          Переходя к моментам и скоростям, учитывая связь между линейной скоростью груза и частотой вращения барабана (2):

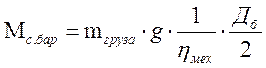                                                                                  (7)

Найдем момент статического сопротивления  созданный весом груза приведенный к оси вращения двигателя на основании равенства мощностей при подъеме груза:

                                                                                                 (8)

где - мощность подводимая с двигателя,  - момент статического сопротивления при подъеме груза, - мощность потерь на трение в редукторе.

Найдем выражение для  мощности потерь на трение в редукторе,  используя  выражение для КПД редуктора при подъеме груза:

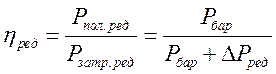
где  -  коэффициент полезного действия механизма барабана,  - полезная мощьность совершаемая редуктором равная мощности подводимой к барабану,  - затрачиваемая мощность складывающаяся из мощности подводимой к барабану и мощности потерь в редукторе.

Откуда:

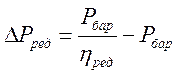
Подставляя в уравнение (8) получим:

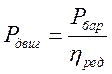
Переходя к моментам и скоростям, учитывая связь между частотой вращения барабана и двигателя (4), и ранее полученное выражение для момента сопротивления приведенного к оси барабана (7):

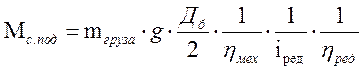
          Подставляя  численные значения, найдем момент статического сопротивления при подъеме:

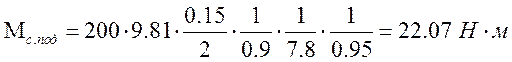
1.2.2 Генераторный (тормозной) режим – при спуске груза.

Проводя рассуждения аналогичные п.2.1 и учитывая, что при спуске груза потери в редукторе и механизме барабана покрываются за счет его потенциальной энергии, можно получить выражение момента для статического сопротивления при спуске груза:        [1, с. 52]

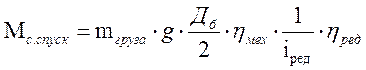
          Подставляя  численные значения, найдем момент статического сопротивления при спуске груза:

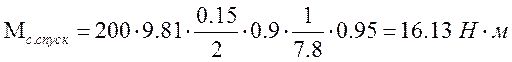
1.3. Построение естественных скоростных и механических характеристик, определение установившихся скоростей при спуске и подъеме.

Естественная механическая характеристика представляет собой зависимость частоты вращения электродвигателя от развиваемого им момента в установившемся режиме работы, при номинальных параметрах питающей сети, нормальных схемах включения и отсутствия добавочных сопротивлений в цепях машины.  [1, c. 62]

          Скоростные характеристики представляют собой зависимости частоты вращения двигателя от тока ротора приведенного к обмотке статора и  тока статора.

          Для расчета и построения статических механических характеристик асинхронных электродвигателей рекомендуется использовать уравнения, полученные на основе упрощенного Г-образной схемы замещения и позволяющие получить достаточную (в пределах 5%) для инженерных расчетов точность.                                                                               

Расчет производится в следующей последовательности:    [2, с. 6]

В соответствии с заданием необходимо учесть перегрев двигателя , для этого воспользуемся выражениями:

где - величины сопротивлений фазных обмоток статора и ротора с учетом перегрева, - сопротивления фазных обмоток статора и ротора при номинальной температуре, - температурный коэффициент сопротивления меди,  - перегрев двигателя.

Активное сопротивление фазной обмотки ротора приводится к обмотке статора:

где - коэффициент трансформации АД.

Определяется суммарное активное сопротивление фазной цепи ротора, приведенное к обмотке статора:

где - активное добавочное сопротивление в цепи фазной обмотки ротора, приведенное к обмотке статора.

          Определяется индуктивное сопротивление рассеяния короткого замыкания:

где - индуктивное сопротивление рассеяния фазной обмотки статора, - индуктивное сопротивление рассеяния фазной обмотки ротора, приведенного к обмотке статора.

          Определяется безразмерный коэффициент:

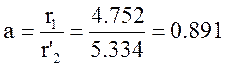
Определяется синхронная скорость вращения АД:

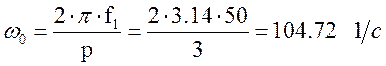
где  - линейная частота тока статора, - число пар полюсов обмотки статора.