









Надстройка Microsoft Excel "Подбор параметра" в решении финансово-экономических задач
Я занимался до сих пор решением ряда задач, ибо
при изучении наук примеры полезнее правил.
(И. Ньютон, "Всеобщая арифметика", 1707 г.)
В финансово-экономической практике нередко приходится сталкиваться с задачами вычислительного характера. Причем, по своей постановке, такие задачи могут быть как прямыми, так и обратными. Решение задач в прямой постановке позволяет ответить на вопрос "что будет, если...", а решение задач в обратной постанове – на вопрос "что надо, чтобы...".
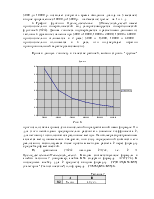
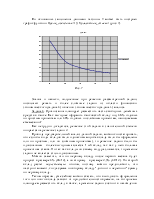
Пример задачи в прямой постановке: вкладчик положил в банк 10000 рублей под 24% годовых. Какая сумма будет на счету вкладчика по истечении 8 месяцев?
При решении данной задачи мы последовательно находим ежемесячную процентную ставку (24%/12=3%), доход по процентам (10000р.´8´3%=2400р.) и, наконец, окончательную сумму вклада (10000р.+2400р.=12400р.). Здесь выполняемые действия и их последовательность диктуются самим условием задачи.
А вот пример задачи в обратной постановке: вкладчик положил в банк 10000 рублей под 24% годовых. По истечении скольких месяцев на счету вкладчика будет сумма в размере 15000р.?
Здесь, в отличие от первой задачи, из условия явно не видно, какие действия ведут к решению задачи. При так называемом арифметическом решении нужно проявить подчас большую изобретательность, чтобы наметить план решения обратной задачи. Каждая новая задача требует зачастую разработки нового плана решения. Для рационализации вычислительного процесса и был придуман метод уравнений, который является основным предметом изучения в алгебре.
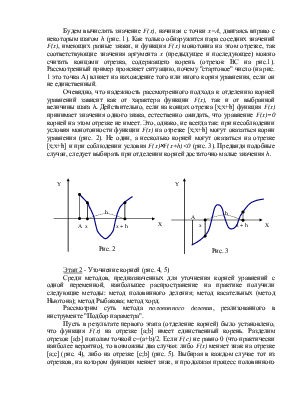
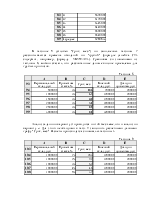
Надстройка Microsoft Excel "Подбор параметра" служит для решения задач в обратной постановке с одним неизвестным. С формальной точки зрения такие задачи описываются уравнением с одной переменной, которое в общем случае можно представить в следующем каноническом виде:
F(x)=0 ,
где функция F(x) определена и непрерывна на интервале [a,b].
Всякое число х, принадлежащее интервалу [a,b] и обращающее функцию F(x) в нуль называется корнем уравнения. Таким образом, можно сказать, что инструмент "Подбор параметра" служит для нахождения корня уравнения х.
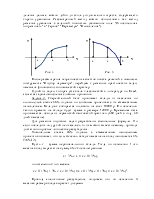
Может возникнуть вопрос: "А если корень уравнения является не единственным?" На этот вопрос ответ будет дан несколько позднее, а сейчас рассмотрим технологию работы с инструментом "Подбор параметра".
Диалоговое окно данного инструмента (вызывается через меню "Сервис", пункт "Подбор параметра") имеет следующий вид:
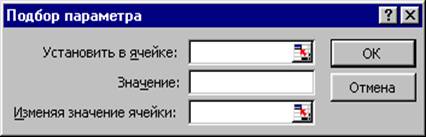 |
В поле "Установить в ячейке" вводится ссылка на ячейку, содержащую левую часть уравнения.
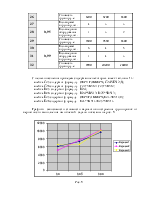
В поле "Значение" непосредственно (т. е. без ссылок на ячейки) вводится правая часть уравнения. Причем правая часть уравнения должна обязательно представлять собой конретное числовое значение. Если правая часть уравнения содержит переменную или какое либо выражение, то такое уравнение должно быть предварительно преобразовано к равносильному виду (в общем случае к каноническому виду F(x)=0).
Пример. Имеем уравнение x2 + 3x = 1 + Sin(x).
Прежде чем переходить к решению данного уравнения, его необходимо предварительно преобразовать к равносильному виду
x2 + 3x - Sin(x) = 1
или к равносильному каноническому виду
x2 + 3x - Sin(x) - 1 = 0 .
В первом случае в поле "Значение" вводится 1, во втором - 0.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.