 |
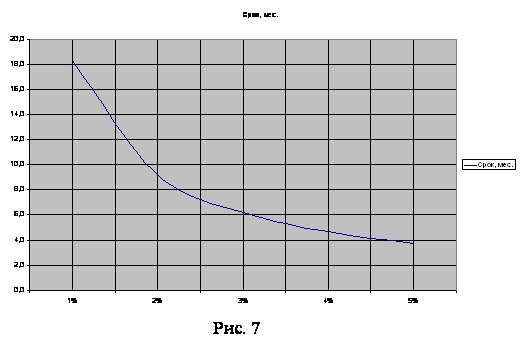
По окончанию заполнения данными таблицы 9 может быть построен график функции Время_ожидания = f(Процентная_ставка) (рис. 7).
Знания и навыки, полученные при решении рассмотренной задачи, позволяют решать и более сложные задачи из области финансово-экономического (задача 3) и военно-экономического (задача 4) анализа.
Задача 3. Организация планирует разместить часть свободных денежных средств в банке. Как выгоднее оформить банковский вклад: под 36% годовых по простым процентам или 30% годовых по сложным процентам, начисляемым ежемесячно?
Как нетрудно догадаться, решение этой задачи в значительной степени опирается на решение задачи 2.
Проводя предварительный анализ данной задачи, можно констатировать, что если бы виды вкладов были одинаковыми (оба вклада были бы оформлены или по простым, или по сложным процентам), то решение задачи было бы однозначным - более выгодным является 1-ый вклад, так как у него большая процентная ставка. Но так как вклады по своему виду различаются, то решение задачи не является столь однозначным.
Можно заметить, что по первому вкладу после первого месяца будет прирост в размере 3% (36/12), а по второму - в размере 2,5% (30/12). Но второй вклад растет нарастающим итогом, поэтому можно предположить, что наступит момент, когда сумма по второму вкладу "догонит и перегонит" сумму по первому вкладу.
Таким образом, уже сейчас можно сказать, что выгодность оформления того или иного вклада зависит от продолжительности времени, на которое мы планируем разместить вклад в банке, а решение задачи состоит в нахождении того момента времени, когда сумма по 1-ому и 2-ому вкладам будет одинаковой. До этого момента времени более выгодным будет являться 1-ый вклад, после этого момента - 2-ой вклад. Исходя из этой информации и надо принимать решение о выборе вида вклада.
Для нахождения "точки равновесия" вкладов проведем следующие рассуждения.
Ставка 36% годовых по простым процентам означает, что первоначальный вклад ежемесячно увеличивается на 3%, т.е. размер вклада составит:
после 1-ого месяца - х + 3% ´ х = x ´ (1+3%),
после 2-ого месяца - х + 3% ´ 2 ´ x = x ´ (1 + 3% ´ 2),
: : : : : : : :
после n-ого месяца - х + 3% ´ n ´ x = x ´ (1 + 3% ´ n).
Ставка 30% годовых по сложным процентам с ежемесячным начислением процентов означает, что по истечении каждого месяца на вклад начисляется 2,5% (30%/12) с нарастающим итогом, но "внутри" каждого месяца начисляются простые проценты.
Дальнейшие рассуждения аналогичны рассуждениям, приведенным в задаче 2. В результате этих рассуждений получаем уравнение
x ´ (1 + 2,5%)[n] ´ (1 + 2,5% ´ (n - [n])) = x ´ (1 + 3% ´ n) ,
которое и будет определять "точку равновесия" вкладов.
Преобразуем данное уравнение к каноническому виду, но перед этим сократим х в правой и левой частях уравнения, т. е. выгодность того или иного вклада не зависит от размещаемой суммы, а зависит только от продолжительности времени его размещения. В результате преобразований получаем уравнение
(1 + 2,5%)[n] ´ (1 + 2,5% ´ (n - [n])) - (1 + 3% ´ n) = 0,
которое может быть решено с помощью инструмента "Подбор параметра".
Для решения уравнения и его исследования составим расчетную таблицу 9 (ячейка D5 содержит формулу =(1+В5)^ЦЕЛОЕ(С5)*(1+B5*(C5-ЦЕЛОЕ(С5)))-(1+А5*С5)
:
Таблица 9
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.