Надстройка Microsoft Excel "Подбор параметра" в решении финансово-экономических задач, страница 7

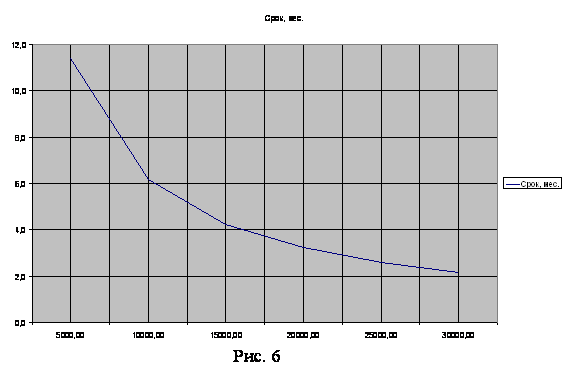
С целью наглядного отображения полученных результатов целесообразно построить график функции Время_ожидания = f(Начальный_вклад) (рис. 6).

Анализ таблицы  3 и построенного графика показывает, что:

1. С увеличением суммы начального вклада сокращается время ожидания вкладчиком желаемого дохода по процентам (что, вообщем-то, само собой разумеется);

2. Начальные "приращения" вклада являются в некотором смысле более "эффективными", чем последующие. Например, первое приращение вклада от 5000 до 10000 р. позволяет сократить время ожидания дохода на 5 месяцев; второе приращение с 10000 до 15000 р. - на 2 месяца; третье - на 1 и т. д.

3. График  функции  Время_ожидания = f(Начальный_вклад) имеет приблизительно гиперболический вид (аппроксимируется гиперболической функцией y=k/x). Данная гипотеза подтверждается и расчетными данными из таблицы 3 (сравните значения при 5000 и 10000, 10000 и 20000, 15000 и 30000 - приблизительно отличаются в 2 раза; 5000 и 15000, 10000 и 30000 - приблизительно отличаются в 3 раза, что подтверждает обратно пропорциональный характер зависимости).

Приняв данную гипотезу в качестве рабочей, можно строить "грубые" прогнозы, избегая громоздких вычислений по разработанной нами формуле. Но для этого необходимо предварительно рассчитать значение коэффициента k, для чего могут использоваться различные методы. Наиболее распространенным является метод наименьших квадратов, но в силу определенной сложности его реализации, воспользуемся более простым методом расчета k через формулу средней арифметической.

Из уравнения y=k/x находим k=y´x, т.е. k = Время_ожидания´Начальный_вклад.  Вводим соответствующие формулы в ячейки таблицы 7 (например, ячейка В83 содержит формулу =A73*C73). В последнюю ячейку (для k среднего) вводим формулу =СРЗНАЧ(B83:B88) (категория "Статистические") или формулу =СУММ(В83:В88)/6.

Таблица 7