Надстройка Microsoft Excel "Подбор параметра" в решении финансово-экономических задач, страница 4

В настоящее время разработано достаточно большое количество численных методов для решения самых разнообразных задач в математической постановке. Задача численного нахождения корней уравнения с одним неизвестным обычно состоит из двух этапов:

1. отделение корней, т. е. нахождение достаточно малых окрестностей, в которых содержится одно значение корня;

2. уточнение корней, т. е. вычисление корней с заданной степенью точности в определенной окрестности.

Суть данных этапов рассмотрим только в самом общем виде, используя  рисунки 1-5.

Этап 1 - Отделение корней (рис. 1-3).

Пусть имеется уравнение F(x)=0 и надо отделить его корни. При этом полезно использовать следующие очевидные положения:

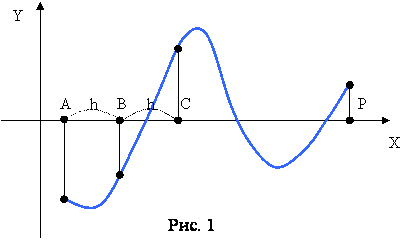а) если непрерывная на отрезке [a,b] функция F(x) принимает на его концах значения разных знаков (т. е. F(a)´F(b)<0), то уравнение имеет на этом отрезке по меньшей мере один корень;

б) если функция F(x) к тому же еще и строго монотонна, то корень на отрезке [a,b] единственный.

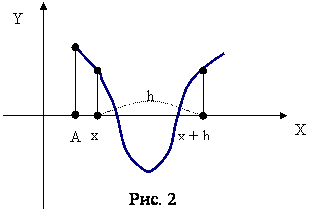
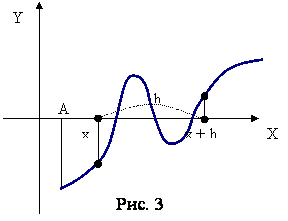
Будем вычислять значение F(x), начиная с точки х=А, двигаясь вправо с некоторым шагом h (рис. 1). Как только обнаружится пара соседних значений F(x), имеющих разные знаки, и функция F(x) монотонна на этом отрезке, так соответствующие значения аргумента х (предыдущее и последующее) можно считать концами отрезка, содержащего корень (отрезок ВС на рис.1). Рассмотренный пример проясняет ситуацию, почему "стартовое" число (на рис. 1 это точка А) влияет на нахождение того или иного корня уравнения, если он не единственный.

Очевидно, что надежность рассмотренного подхода к отделению корней уравнений зависит как от характера функции F(x), так и от выбранной величины шага h. Действительно, если на концах отрезка [x;x+h] функция F(x) принимает значения одного знака, естественно ожидать, что уравнение F(x)=0 корней на этом отрезке не имеет. Это, однако, не всегда так: при несоблюдении условия монотонности функции F(x) на отрезке [x;x+h] могут оказаться корни уравнения (рис. 2). Не один, а несколько корней могут оказаться на отрезке [x;x+h] и при соблюдении условия F(x)´F(x+h)<0 (рис. 3). Предвидя подобные случаи, следует выбирать при отделении корней достаточно малые значения h.

Этап 2 - Уточнение корней (рис. 4, 5)

Среди методов, предназначенных для уточнения корней уравнений с одной переменной, наибольшее распространение на практике получили следующие методы: метод половинного деления; метод касательных (метод Ньютона); метод Рыбакова; метод хорд.

Рассмотрим суть метода половинного деления, реализованного в инструменте "Подбор параметра".

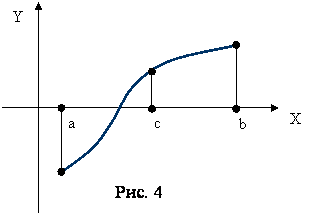
Пусть в результате первого этапа (отделение корней) было установлено, что функция F(x) на отрезке [a;b] имеет единственный корень. Разделим отрезок [a;b] пополам точкой с=(a+b)/2. Если F(c) не равно 0 (что практически наиболее вероятно), то возможны два случая: либо F(x) меняет знак на отрезке [a;c] (рис. 4), либо на отрезке [c;b] (рис. 5). Выбирая в каждом случае тот из отрезков, на котором функция меняет знак, и продолжая процесс половинного деления дальше, можно дойти до сколь угодно малого отрезка, содержащего корень уравнения. Рассмотренный метод можно использовать как метод решения

уравнения с заданной точностью (вспомните поле "Относительная погрешность" в "Сервис"-"Параметры"-"Вычисления").