Признак полного дифференциала. Интегрирование иррациональных функций

1. Признак полного дифференциала.

Рассмотрим криволин.

Обл-ть V наз-ся односвязной, если для  замкнут. контура  из этой обл-ти  пов-ть, целиком лежащая внутри этой обл-ти, и имеющая данный контур своей границей.

Теорема:

Если ф-ии  и их частные производные 1-го порядка непрерывны в некоторой замкнут, огранич. Односвязной обл-ти V, то след. утверждения равносильны:

1)  криволин. по  замкнут. контуру, лежащему внутри обл-ти V равен 0

2) 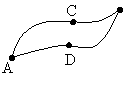 криволин. не зависит от выбора пути, соедин-го (..) A и B обл-ит V.

3)  Выр-е  является полным диф-ом, т.е. где  - опред-ся в обл-ти V

4)  Вып-ся рав-ва

2. Интегрирование иррациональных ф-ий

Интегралы такого вида всегда могут быть приведены от рац. ф-ий при помощи подстановок Эйлера.

а) Если a>0, то  - первая подстановка Эйлера

б) Если с>0, то  - вторая подстановка Эйлера

в) Если  - корни квадратного трехчлена, стоящего под корнем, то

Замечание: подстановки Эйлера ведут обычно к громоздким вычислениям, поэтому их стоит применять, если нет других путей вычисления.