Понятие предела последовательности
Постановка задачи. Пользуясь определением предела последовательности, доказать, что
План решения.
1. По определению число 
называется пределом
числовой последовательности 
, если 
.
Это означает, что 
неравенство 
имеет решение 
.
2. Находим, при каких 
справедливо неравенство
,
т.е. решаем это неравенство относительно .
3. Если решение имеет вид , то – предел числовой
последовательности .
Замечание.
Если решение неравенства нельзя представить в
виде ,
то число не является пределом последовательности.
Задача 1.
Доказать, что 
(указать 
).
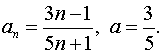
Покажем, что для любого 
существует такой номер , что для
всех .
.
.
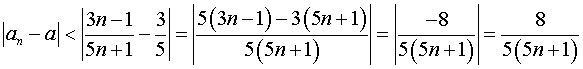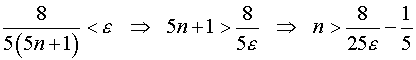Из последнего неравенства следует, что можно выбрать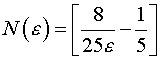 
(квадратные
скобки означают целую часть) и при любых будет выполняться
неравенство . Значит, по определению предела последовательности
.
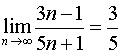Вычисление
пределов вида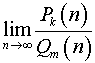 
Постановка задачи. Вычислить предел
,
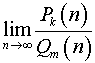где
,
.
План решения.
Здесь 
– многочлен степени 
(бесконечно большая
последовательность порядка 
) и 
– многочлен степени
(бесконечно
большая последовательность порядка 
).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
