1. Вынесем в числителе множитель ![]() , получим
, получим ![]() , где
, где ![]() .
.
2. Вынесем в знаменателе множитель ![]() , получим
, получим ![]() , где
, где ![]() .
.
3. Имеем
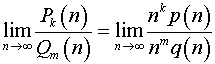 .
.
4. Получаем, что
если ![]() ,
то
,
то 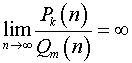 ;
;
если ![]() ,
то
,
то 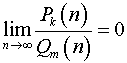 ;
;
если ![]() ,
то по теореме о пределе частного
,
то по теореме о пределе частного
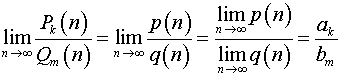 .
.
Задача 2. Вычислить пределы числовых последовательностей.
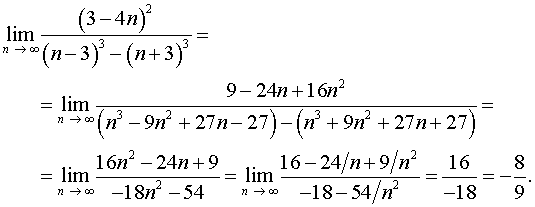
Вычисление пределов вида 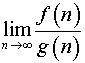
Постановка задачи. Вычислить предел
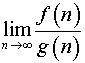 ,
,
где ![]() –
бесконечно большая последовательность порядка
–
бесконечно большая последовательность порядка ![]() и
и ![]() – бесконечно
большая последовательность порядка
– бесконечно
большая последовательность порядка ![]() (
(![]() ).
).
План решения.
1. Вынесем в числителе множитель ![]() , получим
, получим ![]() , где
, где ![]() .
.
2. Вынесем в числителе множитель ![]() , получим
, получим ![]() , где
, где ![]() .
.
3. Имеем
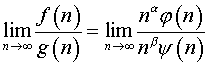 .
.
4. Получаем, что
если ![]() ,
то
,
то 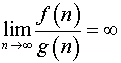 ;
;
если ![]() ,
то
,
то 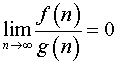 ;
;
если ![]() ,
то по теореме о пределе частного
,
то по теореме о пределе частного
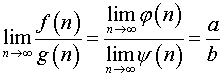 .
.
Задача 3. Вычислить пределы числовых последовательностей.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.