Інтеграли по поверхні. Теорема і формула Стокса. Формула Остроградського-Гауса

Лекція 10

Інтеграли по поверхні

План:

 10.1. Потік рідини через поверхню. Інтеграл по поверхні.

 10.2. Обчислення інтегралів по поверхні.

 10.3. Приклади.

 10.4. Теорема і формула Стокса.

 10.5. Формула Остроградського-Гауса.

 10.6. Запитання для самоперевірки.

Українсько-російський словник вжитих в лекції слів, які в мовах мають різне звучання.

Течія –  течение Виклад –  изложение Нестислива – несжимаемая Обумовлене – обусловленное Розташованих –          – расположенных Досить – достаточно З погляду – с точки зрения Реальний – действытельный Вважається – считается Дотична – касательная

Напрямний –       – направляющий Одержана – полученная Звернена – обращена Позитивний –             –  положительный Варто – стоит Передбачається –          – предусматривается Твірні – образующие Відбувається – происходит Доданок – слагаемое Співпадає – совпадает

Довільна – произвольная Зовнішнє – внешнее Повинна – должна Прирікає – обрекает Зважаючи – обращая внимание Наявність – наличие Ліворуч – по левую руку Складної – сложной Застосуємо – применяем Безсумнівно – несомненно Придатний – нужный,                   подходящий

Математичні факти з попередніх розділів, які використовуються в даній лекції.

1. Кількість рідини, яка протече при ламінарній течії з швидкістю  вздовж труби через перпендикулярний перетин площею s за час t буде дорівнювати .

2. Якщо поверхня задана рівнянням , то рівняння нормалі має вигляд 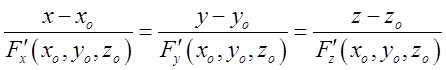 , а напрямний вектор нормалі є . 2. Якщо поверхня задана рівнянням , то рівняння нормалі має вигляд 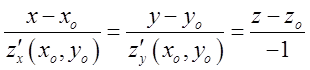 , а напрямний вектор нормалі є . 

Норма (довжина) цього вектора є 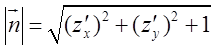. Пронормувати вектор  означає знайти вектор одиничної довжини і співнаправлений з . Для цього досить вектор  поділити на його довжину: 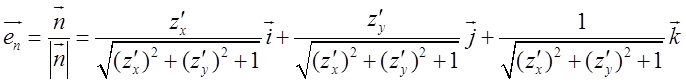. Очевидно даний вираз ми можемо переписати так: , де  – кути, які утворює   відповілно з вісями Ох, Оу, Oz.

3. Проекція площі S трикутника АВС на площину , як це видно з рисунка, дорівнює

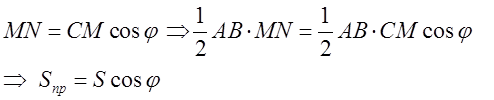, де  – кут між площиною  і площиною трикутника АВС. В частинному випадку, коли основа трикутника АВ ледить в площині ,  це слідує з того, що Цей факт носить загальний характер:  – де S площа якої завгодно плоскої фігури,   - її проекція на деяку площину,  – кут між площинами.

10.1. Потік рідини через поверхню. Інтеграл по поверхні.

В попередній лекції ми розвязували задачу на обчислення потоку рідини через криву лінію L і виявилось, що величина потоку (пригадаємо: потік – це кількість рідини, яка протікає через щось за одиницю часу) визначається через криволінійний інтеграл по кривій L . А яким інтегралом буде обчислюватись величина потоку через деяку поверхню S? Мабуть для цього прийдеться вводити нове математичне поняття – поверхневий інтеграл. Цим ми зараз і займемось.  Поставимо фізичну задачу. Нехай маємо деяку течію рідини. Говорять, що течія встановилася, якщо швидкість часток рідини, що протікають через дану точку, залежить тільки від цієї точки і не залежить від часу. Таким чином, в кожній точці M(x,y,z) області, в якій відбувається течія, заданий вектор  –  швидкість частки рідини в цій точці і ми можемо сказати, що нам задано векторне поле – поле швидкостей рідини. Проекції вектора  на осі координат будуть функціями координат точки М(x,y,z).

Заради простоти викладу, вважатимемо густину рідини  постійною і рівною, одиниці.  Обчислимо кількість рідини, що протікає за одиницю часу через задану поверхню;

Розв’язок почнемо з розгляду найпростішого випадку. Нехай швидкість течії рідини у всіх точках однакова за величиною і напрямком . Тоді зрозуміло, що потік (позначимо його через К) рідини  через прямокутник , розташований у площині, перпендикулярній до вектора швидкості, буде дорівнювати добутку площі прямокутника на величину швидкості: .

Ми розглядаємо нестисливу рідину, а тому зрозуміло, що скільки рідини ввійшло в зображену на рис 10.1 призму (бічні грані цієї призми вважаємо непрникливими) через прямокутник ,  – стільки ж її й вийшло через поверхню прямокутника  ABCD який утворює з попереднім прямокутником                                                                                                                  Рис.10.1.                                                  кут .  Такий же кут  утворює і  нормаль, проведена до ABCD   з     вектором швидкості  . Якщо позначити через S площу прямокутника ABCD, а площу прямокутника  терез , то із співвідношень  при  випливає, що , а це ж  . Тому можна записати:

                        ,                                                                        (10.1)

 де  – проекція швидкості   на нормаль .

Прямокутні поверхні ми розглядали винятково для наглядності. Звичайно   формула (10.1)  вірна не тільки для прямокутника, але і для будь-якої площадки, розташованої в площині, нормаль до якої утворить той же кут  зі швидкістю .

Перейдемо тепер до загального випадку. Нехай у деякій області задане поле швидкостей рідини, обумовлене векторною функцією

Візьмемо деяку поверхню S. Підрахуємо потік рідини через цю поверхню. Для цього розіб'ємо дану поверхню довільним образом на п частин; площі одержаних ділянок позначимо  ,,...,.  На кожній площадці виберемо по двільній точці . Вважаючи ці площадки плоскими і припускаючи, що в межах кожної площадки швидкість рідини залишається постійною, а саме рівною швидкості в точці , можемо написати наближене значення виразу для потоку рідини