де S-границя
області ![]() і інтегрування по S проводиться по її зовнішній стороні (
і інтегрування по S проводиться по її зовнішній стороні (![]() -напрямні косинуси зовнішньої нормалі).
Формула (10.17) називається формулою Остроградского-Гауса.
-напрямні косинуси зовнішньої нормалі).
Формула (10.17) називається формулою Остроградского-Гауса.
Доведення. Ідея
доведення така ж як і при доведенні формули Гріна, але тут будемо потрійний
інтеграл зводити до поверхневого. Візьмемо в просторі Охуz область ![]() обмежену замкнутою поверхнею S, що перетинається
з всякою прямою паралельною координатним вісям не більш ніж у двох точках.
Перетворимо потрійний інтеграл
обмежену замкнутою поверхнею S, що перетинається
з всякою прямою паралельною координатним вісям не більш ніж у двох точках.
Перетворимо потрійний інтеграл 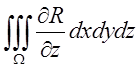 в поверхневий. Зробимо
проекціювання поверхні на площину хОу. Для цього проведем циліндричну поверхню
з твірними, які дотикаються до області
в поверхневий. Зробимо
проекціювання поверхні на площину хОу. Для цього проведем циліндричну поверхню
з твірними, які дотикаються до області![]() і
перпендикулярні до площини хОу. Ця циліндрична поверхня дотикається до області
і
перпендикулярні до площини хОу. Ця циліндрична поверхня дотикається до області ![]() по лінії L і розбиває замкнуту поверхню на дві незамкнуті
по лінії L і розбиває замкнуту поверхню на дві незамкнуті ![]() кожна з який
перетинається з будь-якою прямою, паралельною вісі Оz, не більше
ніж в одній точці. (Це забезпечить нам однозначність
проектування на координатну площину хОу). Нехай область D є проекція поверхонь
кожна з який
перетинається з будь-якою прямою, паралельною вісі Оz, не більше
ніж в одній точці. (Це забезпечить нам однозначність
проектування на координатну площину хОу). Нехай область D є проекція поверхонь ![]() ,
а значить і всієї області
,
а значить і всієї області ![]() на площину Оху,
а
на площину Оху,
а ![]() – рівняння поверхонь
– рівняння поверхонь ![]() . Інтегруючи спочатку по z одержимо
. Інтегруючи спочатку по z одержимо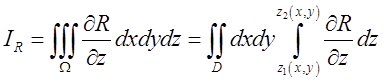 =
=
=
=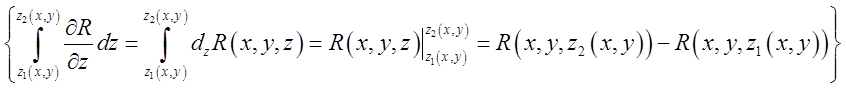 =
=
=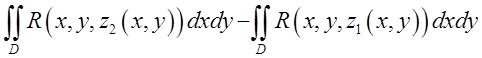 .
.
|
|
Так как плоска область D є проекцією на площину Оху і поверхні ![]() , і
поверхні
, і
поверхні![]() , то подвійні інтеграли в правій частині
слугують виразами для інтегралів
, то подвійні інтеграли в правій частині
слугують виразами для інтегралів ![]() , узятих по верхніх
сторонах цих поверхонь. А тому
, узятих по верхніх
сторонах цих поверхонь. А тому
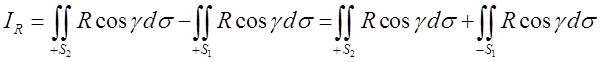 . Тому що верхня
сторона
. Тому що верхня
сторона ![]() і нижня сторона
і нижня сторона ![]() є
зовнішніми
є
зовнішніми
Рис.10.8.
сторонами всієї поверхні S то 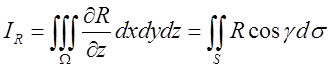 (10.18)
(10.18)
Аналогічно доводяться ще два співвідношення
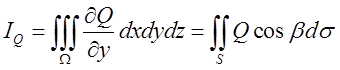 (10.19)
(10.19)
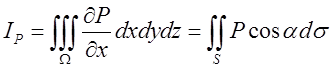 (10.20)
(10.20)
Складаючи почленно рівності (10.18), (10.19), (10.20), ми і приходимо до формули Остроградського . Теорема доведена.
Формула. Остроградского дозволяє замінити потрійний интеграл відповідним інтегралом по поверхні, яка обмежує область інтегрування і, навпаки, інтеграл по замкнутій поверхні замінити потрійним інтегралом по області обмеженою цією поверхнею.
П.5. Обчислити 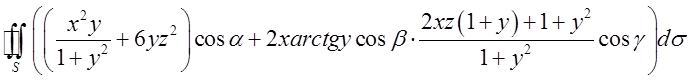
через замкнуту
поверхню обмежену зверху ![]() і знизу
площиною
і знизу
площиною ![]() .
.
Розв’язок. Застосуємо теорему Остроградського. Для (10.17) обчислимо 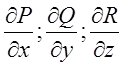 .
.
З виду інтеграла знаходимо: 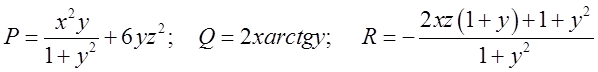 ;
;
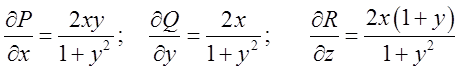 .Обчислимо
.Обчислимо 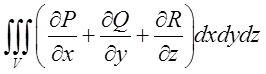 ;
;
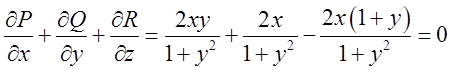 . А це значить, що
. А це значить, що 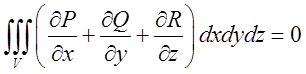 .
.
Відповідь: 0
П.6. Обчислити
криволінійний інтеграл 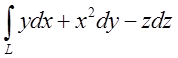 , де
, де ![]() - контур
- контур 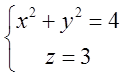 .
.
Розв’язок. Застосуємо теорему Стокса і формулу (10.10). Для цього на коло 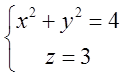 , “натягнемо” яку – небудь
поверхню. Звичайно візьмемо найпростішу – круг. Поверхня буде мати вигляд:
, “натягнемо” яку – небудь
поверхню. Звичайно візьмемо найпростішу – круг. Поверхня буде мати вигляд: 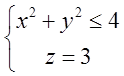 . Для застосування
теореми Стокса обчислимо
. Для застосування
теореми Стокса обчислимо 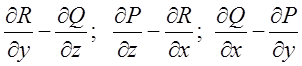 , де
, де ![]()
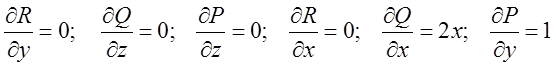 . Тому перші дві
різниці дорівнюють 0,
. Тому перші дві
різниці дорівнюють 0,
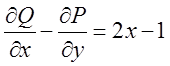 . Підставляючи в
формулу Стокса одержимо:
. Підставляючи в
формулу Стокса одержимо: 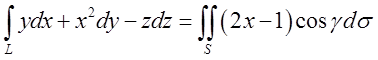 , де S – поверхня
, де S – поверхня 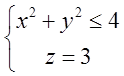 . Так як S паралельна площині
. Так як S паралельна площині![]() то
то ![]() і
і ![]() , як відомо
, як відомо ![]() і поверхневий інтеграл дуже
легко зводиться до подвійного
і поверхневий інтеграл дуже
легко зводиться до подвійного 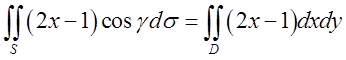 - де
- де ![]() - круг
- круг ![]() , який лежить на площині
, який лежить на площині ![]() . Перейдемо до полярної
системи координат
. Перейдемо до полярної
системи координат
![]() , границі очевидні
, границі очевидні ![]() .
.
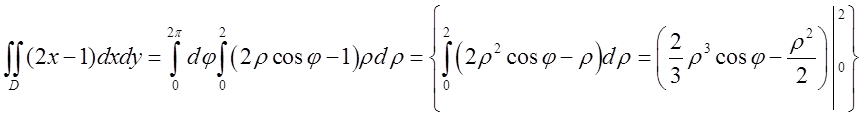 =
=
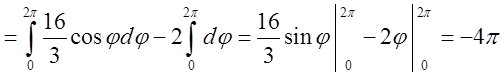 . Відповідь:
. Відповідь: ![]() .
.
Запитання для самоперевірки.
1. Чому дорівнює потік К рідини через поверхню
S, пормаль якої утворює з вектором
швидкості ![]() кут
кут ![]() ?
?
2. З яких пунктів складається розв’язок задачі про знаходження величини потоку К вектора ![]() через поверхню S? Завершіть низку міркувань: 1) розбиваємо поверхню S на елементарні поверхні
через поверхню S? Завершіть низку міркувань: 1) розбиваємо поверхню S на елементарні поверхні ![]() ; 2)...3)...4)....
; 2)...3)...4)....
3.Що таке поверхневий інтеграл?
4. Який фізичний смисл має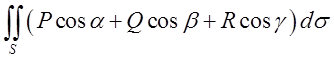 , якщо вектор
, якщо вектор ![]() описує
силове поле?
описує
силове поле?
5. Що означає 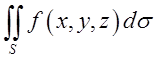 , якщо
, якщо
![]() – є функція розподілу поверхневої маси?
– є функція розподілу поверхневої маси?
6. Що означає 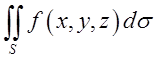 , якщо
, якщо
![]() – є функція розподілу електричного заряду?
– є функція розподілу електричного заряду?
7. Що означає 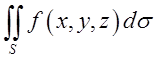 , якщо
, якщо
![]() ?
?
8. Як обчислюється 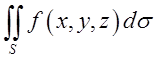 ,
якщо
,
якщо ![]() – функція, яка виражає рівняння поверхні?
– функція, яка виражає рівняння поверхні?
9. При проектуванні двохстороньої поверхні S на площину хОу, яка сторона вважається додатньою, а яка відємною?
10. Як зміниться інтеграл 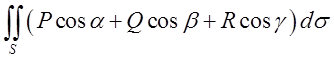 при інтегруванні по іншій стороні
поверхні?
при інтегруванні по іншій стороні
поверхні?
11. Чому дорівнює поверхневий інтеграл по поверхні S, якщо при проектуванні на площину хОу ця поверхня проектується у відрізок?
12. Сформулюйте теорему і запишіть формулу Стокса.
13. Що пов’язує між собою формула Стокса?
14. Сформулюйте теорему і запишіть формулу Остроградського.
15. Що пов’язує між собою формула Остроградського?
Розвязати самостійно.
10.1. Обчислити поверхневі інтеграли першого типу:
а)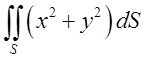 , де S – сфера
, де S – сфера ![]() . Відп.
. Відп.
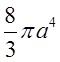 .
.
б) 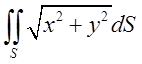 , де S – бокова поверхня конуса
, де S – бокова поверхня конуса
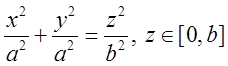 . Відп.
. Відп.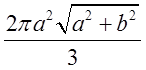 .
.
10.2. Обчислити 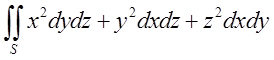 , де S – зовнішня сторона поверхні напівсфери
, де S – зовнішня сторона поверхні напівсфери
![]() . Відп.
. Відп. ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.