Інтеграли по поверхні. Теорема і формула Стокса. Формула Остроградського-Гауса, страница 4

Розв’язок. Нехай радіус сфери R. В центрі сфери розмістимо прямокутну декартову систему координат. Тоді її рівняння буде . Який завгодно діаметр сфери буде її віссю симетрії, а тому за фіксований візьмемо діаметр, який співпадає з віссю Оу, рис. 10.5. Квадрат віддалі довільної точки від вісі Оу буде . За умовою ця функція є поверхнева густина, а тому маса сфери буде 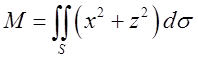. Маса кожного із вісьми сегментів сфери, які розміщаються в кожному із вісьми

 октантів буде однакова, а тому доцільно обчислити її при , тобто для першого октанту. Згідно з (10.7) маємо 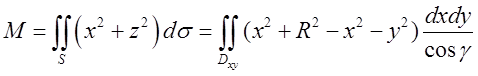. – це косинус кута між віссю Oz та векторм нормалі до поверхні , в нашому випадку . Знайдемо вектор нормалі . Для сфери це буде . Напрямний Рис.10.5.                                                                                                                                  вектор вісі Оz , а косинус кута між цими векторами знаходимо

                                                                    з скалярного добутку

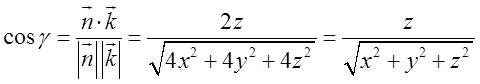. Замінимо , підставимо в інтеграл і одержимо 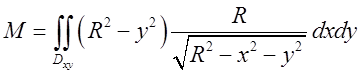. Областю інтегрування є чверть круга при . Границі інтегрування в подвійному інтегралі очевидні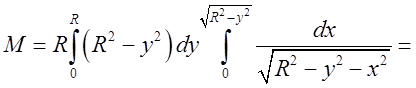

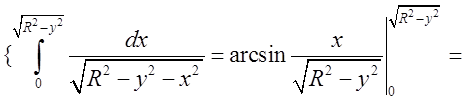
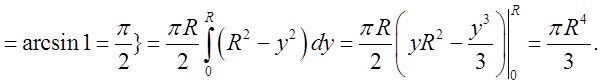
Відп. 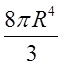(одиниць маси)

Обчислити поверхневі інтеграли по координатах (інтегрли ІІ-го типу).

П.3. 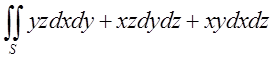, де S – зовнішня сторона піраміди утвореної площинами .

Розв’язок. Зовнішня сторона піраміди, див. рис.10.4, (як, до речі, і внутрішня) складається з чотирьох поверхонь її граней. Крім точки , вершинами піраміди будуть точки перетину площини  з вісями координат . Обчислення інтегралу заданого за умовою перетвориться в обчислення читирьох інтегралів по чотирьох частинах поверхні . Запишемо рівняння цих поверхонь і поведінку змінних та  їх диференціалів на цих поверхнях.

: рівняння ; змінюються всі змінні ;.

 : рівняння ; змінюються лише координати х і z. ; .

: рівняння ; змінюються лише координати х і  у. ; .

: рівняння ; змінюються лише координати z і  у. ; .

Обчислимо інтеграл по кожній з поверхонь.

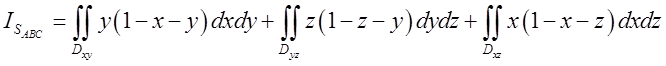. Зрозуміло за умовою на яку координатну площину який доданок проектується і яка змінна повинна виражатись через інші. Всі області мають однаковий вид – рівнобедрені прямокутні трикутники, а тому далі:

. Інтеграли відрізняються один від одного лише видом змінних, тому за величиною вони однакові. Обчислимо перший.

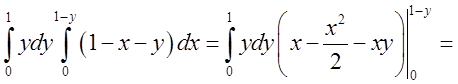
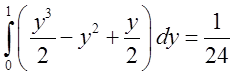.  буде втричі більший, тобто .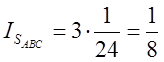

Приступимо до обчислення . Проектувати цю поверхню нікуди не треба бо вона вже лежить на координатній площині. ЇЇ проекції на інші координатні площини є відрізками ОА і ОВ, які не мають площі. Через те із трьох інтегралів 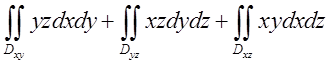два перших дорівнюють нулю із-за рівності нулю площі областей інтегрування, а третій при обчисленні також дасть нуль бо в цій області у=0.  По двох інших областях одержимо такий же результат і з тих же самих причин.

Відповідь. 1/8.

П.4.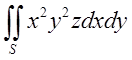 , де S – додатня сторона нижньої половини сфери.

Розв’язок. Обчислювати інтеграл будемо використовуючи проектування поверхні S на площину хОу (на це нас прирікає умова,  де під інтегралом стоїть ). При проектуванні одержимо область  – круг , рис.10.6.  Рівняння  нижньої частини сфери в яному виді буде . Кут – між віссю Оz і нормаллю, для всієї нижньої півсфери буде тупий, а тому .  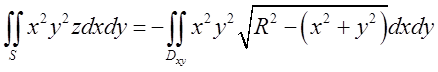При обчисленні цього подвійного інтегралу, зважаючи

                          Рис.10.6.                             на круглу область і наявність в функції виразу , доцільніше перейти до полярної системи координат .Далі одержимо

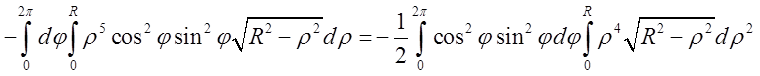
Внутрішній інтеграл обчислимо за допомогою рідстановки    

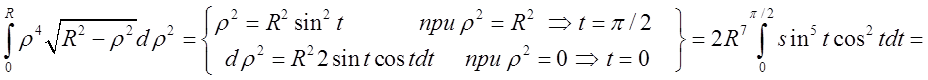
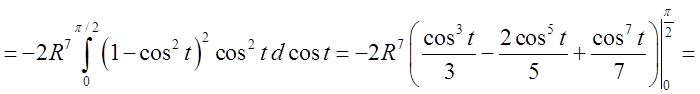
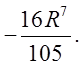
Підставимо значення внутрішнього інтегралу і обчислимо зовнішній інтеграл

.

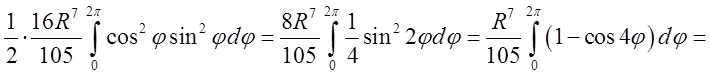
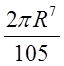Відповідь. .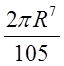

10.4. Теорема і формула Стокса

.                                                                 

Для поверхневих інтегралів має місце формула, аналогічна формулі. Гріна, яка  дозволяє звести обчислення інтеграла по поверхні  S до  обчислення криволінійного інтегралу по контуру L, що обмежує цю поверхню.

Теорема. Нехай функції неперервні  разом зі своїми частинними похідними в деякій тривимірній області. Тоді для будь-якої гладкої поверхні S, що лежить у цій області, має місце формула

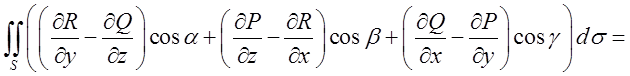
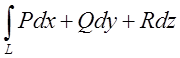      (10.10)

де напрямні косинуси нормалі до поверхні S, а L-границя поверхні.

Ця формула  називається формулою Стокса.