Інтеграли по поверхні. Теорема і формула Стокса. Формула Остроградського-Гауса, страница 5

Напрямок інтегрування по контурі L узгоджується з обраною стороною поверхні S за допомогою наступного наочного правила: якщо людина йде по контурі L в напрямку інтегрування і напрямок від його ніг до голови збігається з напрямком нормалі до обраної сторони поверхні, то ця поверхня повинна залишатися від нього ліворуч (вважається, що обрано праву систему координат, як на рис.10.7 ).

            Доведення.   Доведення цієї теореми за ідеєю схоже на доведення теореми Гріна. Спочатку інтеграл по поверхні

                Рис.10.7.               зводиться до подвійного інтегралу, а потім за допомогою формули Гріна цей подвійний інтеграл зводиться до криволінійного. Припустимо спочатку, що поверхня S має рівняння .  Перетворимо поверхневий інтеграл

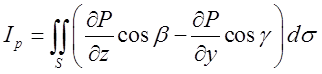,                                                                                        (10.11.)

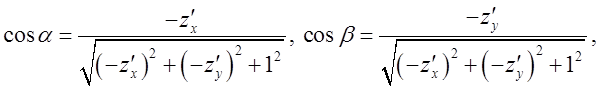
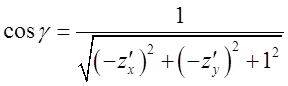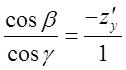
 вважаючи, що S-верхня сторона поверхні; при цій умові . Нормальний вектор до верхньої сторони поверхні має проекції Напрямні косинуси будуть .   Легко обчислити, що . Підставивши знайдене значення  в (10.11), 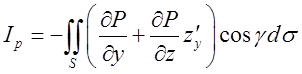                                                                                (10.12)

Приведемо цей поверхневий інтеграл до подвійного. Для цього потрібно в підінтегральній функції замінити змінну z на задане її значення  згідно з рівнянням поверхні. Але при цьому підінтегральна функція виявиться рівній частинній похідній по у від складної функції, що одержиться  з після підстановки  замість z. Дійсно,

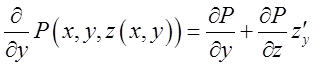                                                                                           (10.13).

 Підставляючи (10.13) в (10.12) одержимо

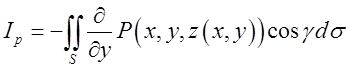,  проектуючи на площину хОу (згадаймо, що ) матимемо 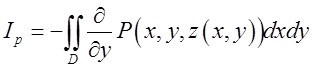, де D – проекція поверхні S на площинк хОу. Застосуємо до цього подвійного інтеграла формулу Гріна 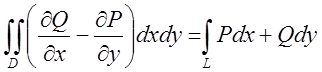   причому у нас .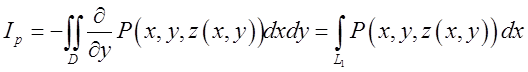, де  – контур який лежить на площині хОу, обмежує область D і є проекцією контура L. Інтегрування проходить в додатньому напрямку обходу контура.

 Для завершення міркування залишилося  зауважити,  що контур L належить поверхні S, тому координати його точок задовольняють рівнянню  і тому значення функції  в точках контуру  дорівнюють значенням  в відповідних точках контуру . Проекції ж відповідних ділянок розбивки контурів  и  на вісь Ох, безсумнівно співпадають. Виходить, збігаються інтегральні суми, побудовані для визначення криволінійних інтегралів по координаті х від функції Р по контурах  и , а тому рівні інтеграли: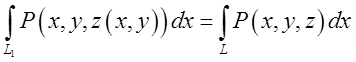. Таким чином ми одержали

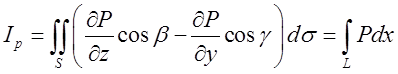                                                                            (10.14)

Аналогічно доводиться справедливість ще двох співвідношень-(рекомендуємо читачу довести їхній самостійно, вибираючи щораз рівняння поверхні в придатному виді):

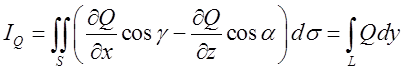                                                                           (10.15)

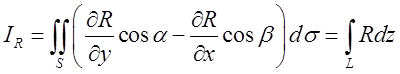                                                                            (10.16)

Додавши почленно рівності (10.14), (10.15) і (10.16), ми одержимо доводжувану формулу.

Формула Стокса дозволяє інтеграл по поверхні замінити відповідним криволінійним інтегралом по границі поверхні і, навпаки, криволінійний інтеграл по замкнутій просторовій лінії замінити інтегралом по поверхні  натягнутій на контур інтегрування.

 Подібно тому як за допомогою формули Гріна в лекції 7 була доведена теорема  про незалежність криволінійного інтеграла в площині від шляху інтегрування, так за допомогою формули Стокса можна дати доказ  відповідної теореми для криволінійних інтегралів по просторових лініях.

Нехай ми маємо інтеграл 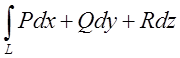 і відомо, що 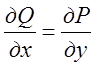;;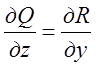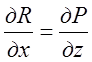. Тоді згідно  з формулою Стокса маємо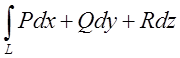 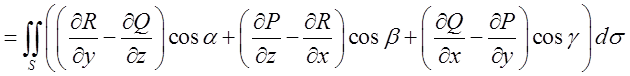 . Але ж кожна з різниць в дужках дорівнює нулеві значить поверхневий інтеграл дорівнює нулеві, тобто 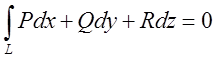 . Але згідно з лемою лекції 7 якщо криволінійний інтеграл по замкнутому контуру дорівнює нулеві, то величина інтегралу не залежить від шляху інтеграла. Що і потрібно було довести.

10.5. Формула Остроградського-Гауса

 Вище ми встановили звязок між поверхневим інтеградом по незамкнутій поверхні S і криволінійним інтегралом по кривій L, яка є границею поверхні S.  Розглянемо тепер зв'язок між інтегралом по замкнутій поверхні і деяким потрійним інтегралом по об’єму, обмеженому цією поверхнею.

Теорема. Нехай функції неперервні  разом зі своїми частинними похідними в деякій замкнутій області , тоді  має місце формула

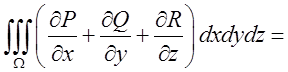
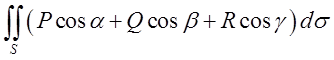                           (10.17)