Рис.10.3.
нормалі ![]() не міняється; це значить, що
площадка
не міняється; це значить, що
площадка ![]() вважається частиною площини, дотичної до
поверхні в точці проведення нормалі. Площадка
вважається частиною площини, дотичної до
поверхні в точці проведення нормалі. Площадка ![]() нахилена
до площини хОу, а значить і до площадки
нахилена
до площини хОу, а значить і до площадки ![]() також
під кутом
також
під кутом ![]() . Тоді за відомою формулою з ел. математики
(
. Тоді за відомою формулою з ел. математики
(![]() , де
, де ![]() –
проекція площі S на площину, в
якій розташовано
–
проекція площі S на площину, в
якій розташовано ![]() ,
, ![]() –
кут між ними ) маємо:
–
кут між ними ) маємо: 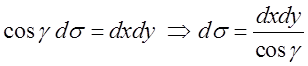 .
(*)
.
(*)
Наша задача – знайти ![]() .
Для цього треба знайти напрямний вектор нормалі до поверхні. Пригадаємо вид
рівняння нормалі до поверхні
.
Для цього треба знайти напрямний вектор нормалі до поверхні. Пригадаємо вид
рівняння нормалі до поверхні ![]() в точці
в точці ![]()
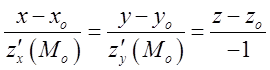 . Як бачимо, напрямним
вектором нормалі в точці
. Як бачимо, напрямним
вектором нормалі в точці ![]() є вектор
є вектор ![]() , а якщо в довільній точці – то
, а якщо в довільній точці – то ![]() . Косинус кута
. Косинус кута ![]() між
віссю Оz і
між
віссю Оz і ![]() знайдемо
з скалярного добутку напрямного вектора вісі Oz
знайдемо
з скалярного добутку напрямного вектора вісі Oz ![]() і
і ![]() . Врахуємо, що кут
. Врахуємо, що кут ![]() гострий,
тобто
гострий,
тобто ![]() . А тому
. А тому 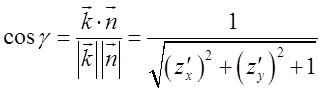 .
Підставимо це в (*).
.
Підставимо це в (*).
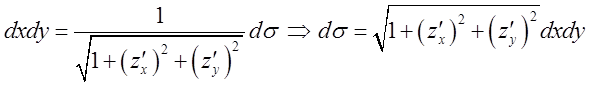 підставивши це, а
також
підставивши це, а
також ![]() в (10.4) одержимо формулу зведення
поверхневого інтегралу типу до подвійного
в (10.4) одержимо формулу зведення
поверхневого інтегралу типу до подвійного
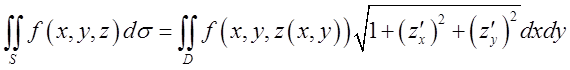 (10.7)
(10.7)
Одержана формула симетрична, тобто якщо
поверхня буде задана у виді![]() , то (10.7) принципово
не зміниться, лише область D буде
знаходитись на площині xOz
, то (10.7) принципово
не зміниться, лише область D буде
знаходитись на площині xOz
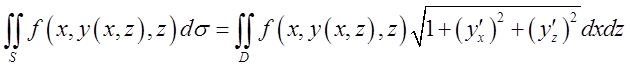 (10.7a)
(10.7a)
А якщо поверхня задана у виді ![]() – проектуємо на площину yOz
– проектуємо на площину yOz
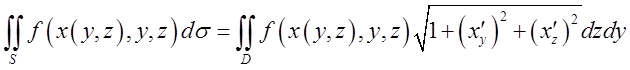 (10.7б)
(10.7б)
Перейдемо до обчислення інтегралів виду (10.3). Розіб’ємо цей інтеграл на три, тобто
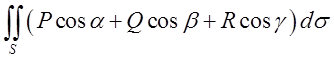 =
=
=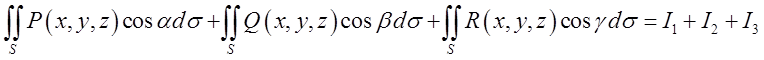
Нехай поверхня задана рівнянням ![]() , знову звернемось до рис. 10.3. Будемо
розрізняти в цієї поверхні верхню сторону (саме до неї проведена нормаль на
малюнку) і нижню сторону. Для верхньої сторони поверхні кут
, знову звернемось до рис. 10.3. Будемо
розрізняти в цієї поверхні верхню сторону (саме до неї проведена нормаль на
малюнку) і нижню сторону. Для верхньої сторони поверхні кут ![]() гострий і, як уже відзначено вище,
гострий і, як уже відзначено вище, ![]() і тому
і тому 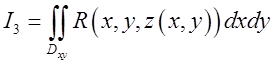 де
де ![]() — як і раніше проекція поверхні S на площину Оху. Зрозуміло, що, беручи
інтеграл по нижній стороні поверхні, ми прийдемо до інтегралу
— як і раніше проекція поверхні S на площину Оху. Зрозуміло, що, беручи
інтеграл по нижній стороні поверхні, ми прийдемо до інтегралу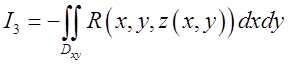 . Аналогічно обчислюються й інтеграли
. Аналогічно обчислюються й інтеграли ![]() та
та![]() .
Потрібно тільки пам'ятати, що у формулах
.
Потрібно тільки пам'ятати, що у формулах ![]() та
та ![]() під
під ![]() ми
розуміємо гострі кути, утворені нормаллю з вісями Ох і Оу. Це
означає, що, розв’язуючи рівняння поверхні відносно х чи у:
ми
розуміємо гострі кути, утворені нормаллю з вісями Ох і Оу. Це
означає, що, розв’язуючи рівняння поверхні відносно х чи у:![]() чи
чи ![]() і
записуючи формули для
і
записуючи формули для ![]() :
: 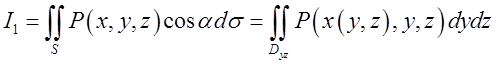 ,
,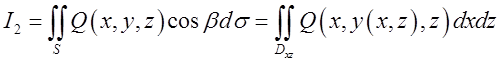 ,
де
,
де ![]() – проекції поверхні S відповідно на площини zОу і xOz, ми щораз беремо інтеграл по тій стороні
поверхні S,
що звернена убік позитивного напрямку осей Ох чи Оу. Якщо нам потрібно
взяти інтеграл по протилежній стороні поверхні, то варто просто змінити знак у
подвійного інтеграла.
– проекції поверхні S відповідно на площини zОу і xOz, ми щораз беремо інтеграл по тій стороні
поверхні S,
що звернена убік позитивного напрямку осей Ох чи Оу. Якщо нам потрібно
взяти інтеграл по протилежній стороні поверхні, то варто просто змінити знак у
подвійного інтеграла.
Якщо при обчисленні якого-небудь із трьох
інтегралів рівняння поверхні не вдається записати в потрібній формі, то
попередньо розбиваємо дану поверхню яа частини, для яких це зробити можна, і
беремо суму інтегралів по цих частинах (звичайно, передбачається, що така
розбивка здійсненна). Зауважимо, що, якщо до складу поверхні S входить ділянка циліндричної поверхні твірні
якої паралельні, наприклад, осі Оz, то інтеграл 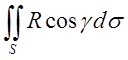 ,
узятий по цій ділянці, дорівнює нулю, так як нормаль буде перпендикулярна до
твірної, і тому
,
узятий по цій ділянці, дорівнює нулю, так як нормаль буде перпендикулярна до
твірної, і тому ![]() , а значить
, а значить ![]() . Геометрично це зрозуміло: подвійний
інтеграл
. Геометрично це зрозуміло: подвійний
інтеграл 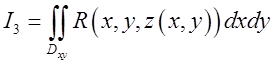 дорівнює
нулю тому, що проекція
дорівнює
нулю тому, що проекція ![]() розглянутої ділянки на площину Оху
є не областю, а лінією. Таким чином ми можемо записати формулу:
розглянутої ділянки на площину Оху
є не областю, а лінією. Таким чином ми можемо записати формулу:
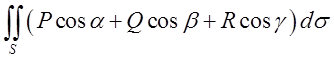 =
=
=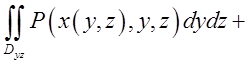
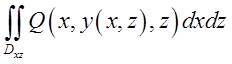 +
+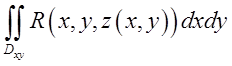 (10.8)
(10.8)
Використовуючи одержані вище формули зведення поверхневого інтегралу до подвійного інтеграли по поверхні (10.3) дуже часто записують так:
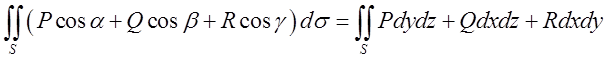 (10.9)
(10.9)
У такому записі (10.9) відразу видно, на яку координатну площину відбувається проектування поверхні S, при інтегруванні кожного доданка. Як ми уже згадували вище, поверхневий інтеграл (10.3) в фориі запису (10.9) називають поверхневим інтегралом другого типу.
10.3. Приклади
Обчислити поверхневі інтеграли по площі поверхні (інтегрли І-го типу).
П.1. 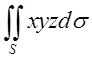 , де S – частина площини
, де S – частина площини ![]() , яка
лежить в першому октанті
, яка
лежить в першому октанті
|
|
Розв’язок. Спроектувавши
поверхню на площину хОу, застосуємо (10.7). Нормаль до площини утворює з віссю Oz гострий кут ![]() ,
, ![]() ,
, ![]() , а
тому
, а
тому
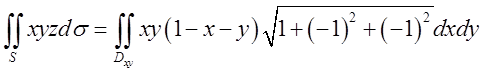 . Область
. Область ![]() – частина площини
– частина площини ![]() ,
обмежена трикутником
,
обмежена трикутником ![]() , а тому
, а тому 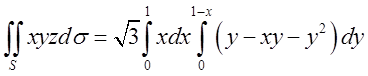 =
=
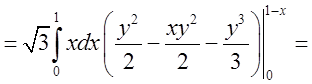
Рис 10.4.
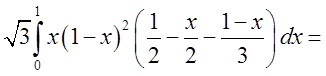
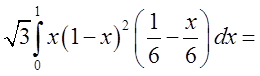
=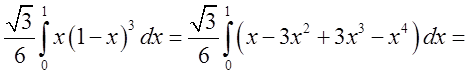
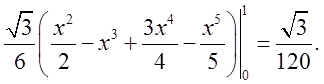
П.2. Знайти масу сфери, якщо її поверхнева густина в кожній точці дорівнює квадрату віддалі цієї точки від деякого фіксованого діаметра сфери.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.