Інтеграли по поверхні. Теорема і формула Стокса. Формула Остроградського-Гауса, страница 2

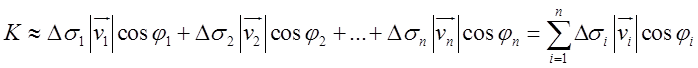
Тут   швидкість у точці , а -кут між нормаллю до поверхні S у точці , і швидкістю .Щоб перетворити отриманий вираз, зауважимо, що   є скалярний добуток вектора  на одиничний вектор нормалі  .

 Позначимо через  кути, утворені нормаллю  з                    осями координат (величини цих кутів залежать, звичайно, від точки ). Одиничний вектор нормалі

                                       Рис. 10.2                                         має своїми проекціями направляючі косинуси  тобто .

Тому , де  –   значення відповідних функцій у точці . 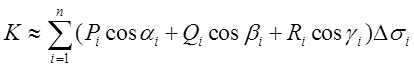                                     (10.2)

Перейшовши до границі при  і за умови, що кожна площадка стягається в точку, ми одержимо вираження для потоку рідини К:

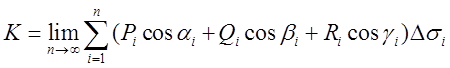 Цю границю запишемо у виді

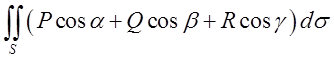                                                   (10.3)

і будемо називати інтегралом по поверхні. У виразі (10.3) і направляючі косинуси нормалі і прекції швидкості на координатні вісі  є функціями координат точки М (х, у, z), а тому вся дужка під інтегралом є якась функція  і найчастіше інтеграл (10.3) подають у виді 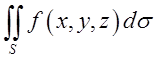. В загальному випадку цьому інтегралові дають таке

Означення. Інтегралом по поверхні (або поверхневим інтегралом) називається границя інтегральної суми

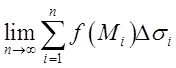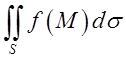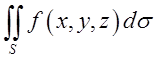==                        (10.4)

 при прямуванні до нуля діаметра кожної площадка розбивки.

            Слід зауважити, що трохи нижче, при обчислені,   інтеграл (10.3) ми перетворимо в інтегрл по добутку координат, який часто називають (за аналогією з схожим криволінійним) поверхневим інтегралом ІІ-го типу, а інтеграл (10.4) поверхневим інтегралом І-го типу.  Фізичний зміст інтегралу (10.3), як ми бачили вище, є потік векторного поля, а якщо замість функції швидкості  взяти функцію сили  (розглядається силове поле) , то (10.3) 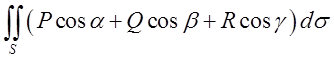= 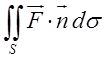буде виражати силовий потік поля через поверхню S.

Фізичний зміст інтегралу (10.4) буде залежати від того, що виражає : якщо  густина електричних зарядів, розташованих на поверхні S, то (10.4) буде виражати сумарний заряд на поверхні; якщо  поверхнева густина маси, розташованої на поверхні S, то (10.4) буде виражати масу всієї поверхні. Звідси зовсім легко одержати формулу для обчислення площі поверхні – досить взяти =1 і

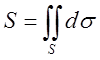 .                                                                  (10.5)

Так, як визначення интеграла по поверхні, по суті справи, аналогічно визначенню подвійного інтеграла то і властивості подвійних інтегралів, без усяких змін переносяться на інтеграли по поверхні. Інтеграла І-го типу це стосується повністю, а знак поверхневого інтеграла другого типу (аналогія з криволінійним) буде залежати від напрямку вектора нормалі до поверхні. Якщо ми його змінимо на протилежний, то зміниться кут між векторами  з  на , а це призведе до зміни знаку скалярного добутку  і зміни знаку всього інтегралу,

З фізичної  точки зору  зміна знака поверхневого інтеграла, (10.3) з погляду задачі про обчислення потоку рідини пояснюється так: на різних ділянках поверхні S рідина може протікати як у напрямку обраної нормалі, так в протилежному і якщо потік К позитивний, то в обраному  напрямку рідини протікає більше, ніж у протилежному, а якщо негативний, то навпаки. Зрозуміло, що в реальному світі всяка поверхня має дві сторони і в подальшому ми й будемо розглядати лише двосторонні поверхні (хоча є й односторонні – знаменитий лист Мьобіуса).

            При зміні напрямку нормалі на протилежний, ми від поверхневого інтегралу по одній стороні поверхні переходимо до поверхневого інтегралу по протилежній стороні, а значить можемо записати для (10.3) дуже важливу властивість

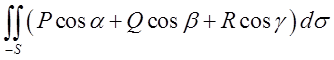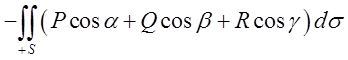=                          (10.6)

10.2. Обчислення інтегралів по поверхні

Як раніше для обчислення кратних і криволінійних інтегралів ми їх зводили до звичайних одновимірних визначених інтегралів, так і тепер спробуємо поверхневий інтеграл звести до обчислення нам уже відомих подвійних інтегралів.

Нехай маємо інтеграл (10.4) тобто інтеграл І-го типу 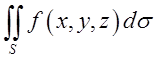, причому S гладенька поверхня, рівняння якої має вигляд . Те, що поверхня гладенька означає, що неперервні. Візьмемо елемент площі  області D і спроектуємо його на поверхню S ( рис 10.3). Площа цієї проекції . Проведемо нормаль  до площадки  так, щоб вона утворювала гострий кут  з віссю Oz. Будемо вважати, що в межах площадки напрямок