Лекція 6
План.
1. Визначений інтеграл.
2. Властивості визначеного інтегралу.
1. Визначений інтеграл
ЗАДАЧІ, ЩО ПРИВОДЯТЬ ДО ПОНЯТТЯ ВИЗНАЧЕНОГО ІНТЕГРАЛА:
1. Нехай на відрізку ![]() задана безперервна функція
задана безперервна функція ![]() . Назвемо криволінійною трапецією
область, обмежену графіком функції
. Назвемо криволінійною трапецією
область, обмежену графіком функції ![]() , віссю Ох і
ординатами х = а, х = b.
, віссю Ох і
ординатами х = а, х = b.
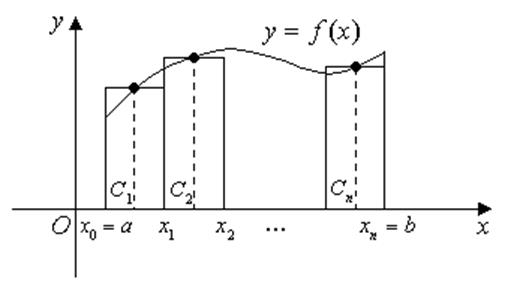
Потрібно обчислити площу цієї трапеції. Для цього розіб'ємо криволінійну трапецію на вузькі смужки, провівши ординати
![]() .
.
На кожному
відрізку ![]() виберемо проміжну крапку
виберемо проміжну крапку ![]() . Площу кожної смужки можна приблизно
вважати рівною площі прямокутника з основою
. Площу кожної смужки можна приблизно
вважати рівною площі прямокутника з основою ![]() і
висотою
і
висотою ![]() , тобто
, тобто
![]() .
.
Отже, площа всієї криволінійної трапеції приблизно дорівнює сумі площ цих прямокутників, тобто
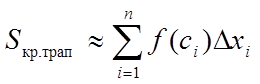 .
.
Ніж дрібніше
будемо розбивати відрізок ![]() , тобто чим вужчими
будуть смужки, тим точніше сума площ прямокутників дасть шукану площу трапеції.
Іншими словами,
, тобто чим вужчими
будуть смужки, тим точніше сума площ прямокутників дасть шукану площу трапеції.
Іншими словами,
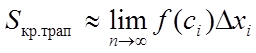 ,
,
де n – число крапок розподілу
відрізка ![]() .
.
2. Розглянемо іншу задачу.
Нехай крапка
рухається по прямій, причому її миттєва швидкість у момент t дорівнює v(t).
Знайти шлях, пройдений крапкою за проміжок часу ![]() .
.
Розіб'ємо
проміжок часу ![]() на n частин:
на n частин:
![]() .
.
Якщо проміжки
досить малі, то можна приблизно вважати швидкість протягом цих проміжків часу постійною.
Тому шлях, пройдений за проміжок ![]() , приблизно виражається
формулою
, приблизно виражається
формулою
![]()
де ci – будь-який
момент часу на проміжку ![]() .
.
Отже, весь пройдений шлях виражається формулою
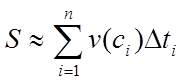 .
.
Ця формула вірна лише приблизно. Але чим менше будуть проміжки часу, тим точніше буде ця формула, іншими словами,
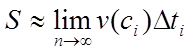 .
.
Таким чином, обидві задачі мають ту саму математичну схему, що складається в наступному.
Нехай на відрізку
![]() задана функція
задана функція ![]() .
Розіб'ємо інтервал
.
Розіб'ємо інтервал ![]() на n частин крапками
на n частин крапками
![]() .
.
У кожному елементарному відрізку розбивки виберемо довільним образом крапки ci і обчислимо значення функцій у цих крапках, тобто знайдемо
![]() .
.
Кожне значення
функції ![]() помножимо на довжину
помножимо на довжину ![]() відповідного відрізка. Складемо суму всіх
цих добутків:
відповідного відрізка. Складемо суму всіх
цих добутків:
![]() , або
, або
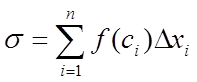 .
.
Цю суму називають
інтегральною сумою для функції ![]() на
відрізку
на
відрізку ![]() .
.
Знайдемо межу
цієї суми при прагненні до нуля найбільшої різниці ![]() , при
цьому число відрізків розбивки необмежено зростає
, при
цьому число відрізків розбивки необмежено зростає
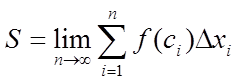 .
.
Ця межа (якщо
вона існує) називається визначеним інтегралом функції ![]() по відрізку
по відрізку ![]() і
позначається
і
позначається 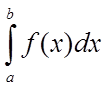 :
:
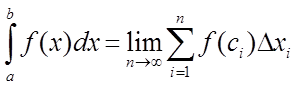 .
.
Отже, визначеним
інтегралом функції ![]() по відрізку
по відрізку ![]() називають межу інтегральних сум за умови,
що найбільший відрізок розбивки прагне до нуля.
називають межу інтегральних сум за умови,
що найбільший відрізок розбивки прагне до нуля.
З задачі (1)
випливає геометричний зміст визначеного інтеграла – це площа криволінійної
трапеції, обмеженої зверху підінтегральною функцією ![]() , знизу
– віссю Ох, а з боків прямими х = а, х = b.
, знизу
– віссю Ох, а з боків прямими х = а, х = b.
З задачі (2) випливає, що шлях S, пройдений крапкою за проміжок часу від t = а до t = b , дорівнює визначеному інтегралові від швидкості v(t):
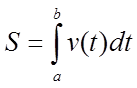 .
.
Провівши
міркування, аналогічні попереднім, можна показати, що робота перемінної сили ![]() , що діє на відрізку
, що діє на відрізку ![]() , дорівнює визначеному інтегралові від
величини
, дорівнює визначеному інтегралові від
величини ![]() сили, узятому по відрізку
сили, узятому по відрізку![]() :
:
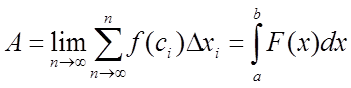 .
.
Маса
неоднорідного стрижня на відрізку ![]() дорівнює визначеному
інтегралові від щільності γ(х):
дорівнює визначеному
інтегралові від щільності γ(х):
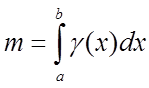 .
.
2. Властивості визначеного інтегралу
1. Інтеграл від алгебраїчної суми функцій дорівнює алгебраїчній сумі інтегралів:
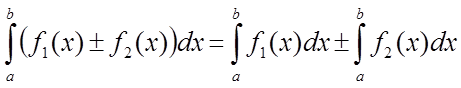 .
.
2. Постійний множник виноситься за знак інтеграла
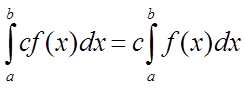 .
.
3. 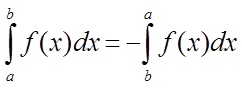 .
.
4. Якщо
функція ![]() інтегрується на
інтегрується на ![]() і
і
![]() , то
, то
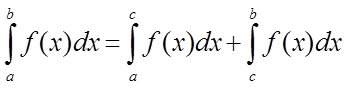 .
.
5. «Теорема
про середнє». Якщо функція ![]() безперервна на відрізку
безперервна на відрізку
![]() , то існує крапка
, то існує крапка ![]() така,
що
така,
що
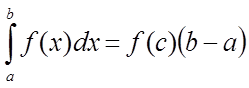 .
.
6. Оцінка
інтеграла. Якщо m і M – відповідно найменше і найбільше значення
функції ![]() на відрізку
на відрізку ![]() ,
, ![]() , то
, то
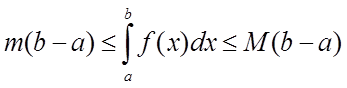 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.