Лекція 1
План:
1. Основні поняття.
2. Задача Коші. Теорема існування та одиничності для диференційних рівнянь 1-го порядку.
3. Основні типи диференціальних рівнянь 1-го порядку що інтегруються в квадратурах.
3.1. рівняння із розділюючимися перемінним;
3.2. однорідні диференціальні рівняння.
1. Основні поняття.
Диференціальним рівнянням називається рівняння, що зв'язує незалежну перемінну, невідому функцію і її похідні:
![]() . (1)
. (1)
Вирішити диференціальне рівняння, означає знайти невідому функцію, при підстановці якої в рівняння, вона звертає його в тотожність.
Наприклад: дане диференціальне рівняння
![]() . (2)
. (2)
Показати, що його рішенням є функції:
![]() .
.
а) підставимо ![]() в
рівняння, знайшовши для цього
в
рівняння, знайшовши для цього ![]() і
і ![]() .
.
![]() .
.
б) ![]() ,
, ![]() і
і ![]() .
.
![]() .
.
в) ![]() .
.
![]() ,
, ![]() .
.
![]() .
.
Порядком рівняння називається порядок вищої похідної, що входить у рівняння.
Наприклад,
рівняння ![]() – рівняння 3-го порядку.
– рівняння 3-го порядку.
Рішення диференціального рівняння, що містить стільки довільних постійних, який порядок рівняння, називається загальним рішенням.
![]() – загальне рішення рівняння (2).
– загальне рішення рівняння (2).
На практиці для визначення довільних постійних задаються початкові умови:
для рівняння 1-го порядку – при ![]() ,
,
або 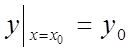 ;
;
для рівняння 2-го порядку – при ![]() ,
,
або 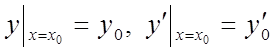 .
.
Диференціальні рівняння, що містять невідому функцію від однієї перемінної, називають звичайними.
2. Задача Коші. Теорема існування та одиничності для диференціальних рівнянь 1-го порядку.
Диференціальне рівняння першого порядку має вигляд
![]() (3)
(3)
або розв'язане відносно ![]() :
:
![]() (4)
(4)
Теорема про існування й одиничність рішення диференціального рівняння першого порядку (теорема Коші) (без доказу)
Якщо в рівнянні
(4) функція ![]() і її похідна
і її похідна ![]() по у
безперервні в деякій області D на площині ХОY, що містить деяку
крапку
по у
безперервні в деякій області D на площині ХОY, що містить деяку
крапку ![]() , то існує єдине рішення цього рівняння
, то існує єдине рішення цього рівняння ![]() , що задовольняє умові: при
, що задовольняє умові: при ![]() .
.
Геометричний
зміст теореми полягає в тому, що існує функція, і причому єдина, ![]() , графік якої проходить через крапку
, графік якої проходить через крапку ![]() . Умова, що при
. Умова, що при ![]() функція
у повинна дорівнювати заданому числу у0, називається
початковою умовою.
функція
у повинна дорівнювати заданому числу у0, називається
початковою умовою.
Визначення 1. Загальним рішенням диференціального рівняння
першого порядку називається функція ![]() , що залежить від
однієї довільної постійної С и задовольняюча рівнянню.
, що залежить від
однієї довільної постійної С и задовольняюча рівнянню.
Причому, якщо при рішенні рівняння (2) отримане співвідношення виду
![]() ,
,
не розв'язане відносно у, то говорять, що отримано загальний інтеграл диференціального рівняння.
Визначення 2. Приватним рішенням називається будь-яка функція
![]() , що виходить із загального рішення
, що виходить із загального рішення ![]() , якщо довільному постійному С
додати визначене значення С=С0.
, якщо довільному постійному С
додати визначене значення С=С0.
Геометрично загальний інтеграл являє собою безліч кривих (інтегральних кривих), що залежать від довільної постійної С.
Приватному інтегралові відповідає одна крива, що проходить через задану крапку.
3. Основні типи диференціальних рівнянь 1-го порядку що інтегруються в квадратурах: із розділюючимися перемінними, однорідні диференціальні рівняння
3.1. Рівняння із розділюючимися перемінними
Рівняння виду ![]() називається рівнянням із розділюючимися перемінними, якщо функції
називається рівнянням із розділюючимися перемінними, якщо функції ![]() і
і ![]() є
добутками функцій залежних від однієї змінної, тобто
є
добутками функцій залежних від однієї змінної, тобто
![]() (5)
(5)
і розділимо обидві частини останньої
рівності на ![]() :
:
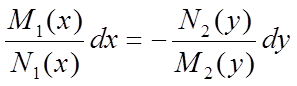 .
.
Одержимо рівняння з розділеними перемінними; взявши інтеграл від лівої і правої частин рівняння (7), одержимо загальне рішення рівняння (5):
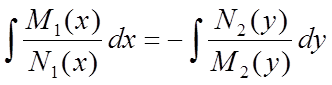
![]() – загальне рішення.
– загальне рішення.
Наприклад:
вирішити рівняння ![]() – рівняння з розділюючимися
перемінними.
– рівняння з розділюючимися
перемінними.
Перепишемо рівняння:
![]() .
.
Щоб розділити перемінні, розділимо на добуток ху обидві частини останньої рівності
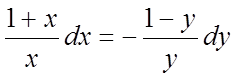
і візьмемо інтеграл від лівої і правої частин:
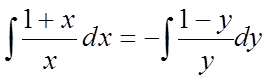 ,
,
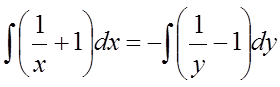 ,
,
![]() –
одержимо загальний інтеграл вихідного рівняння (рішення отримане в неявному
виді).
–
одержимо загальний інтеграл вихідного рівняння (рішення отримане в неявному
виді).
3.2. Однорідні диференціальні рівняння першого порядку
Визначення 1. Функція ![]() називається однорідною функцією n-го
виміру щодо перемінних х та у, якщо при будь-якому λ
виконується умова:
називається однорідною функцією n-го
виміру щодо перемінних х та у, якщо при будь-якому λ
виконується умова:
![]() .
.
Наприклад,
функція ![]() – однорідна функція 2-го виміру. Функція
– однорідна функція 2-го виміру. Функція 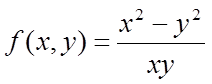 – однорідна функція 0-го виміру.
– однорідна функція 0-го виміру.
Визначення 2. Диференціальне рівняння першого порядку
![]() (6)
(6)
називається однорідним
відносно х та у, якщо функція ![]() є
однорідна функція нульового виміру відносно х та у.
є
однорідна функція нульового виміру відносно х та у.
Рішення однорідного рівняння
За умовою функція
![]() – нульового виміру, тобто
– нульового виміру, тобто ![]() . Поклавши в цій тотожності
. Поклавши в цій тотожності 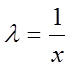 , одержимо:
, одержимо:
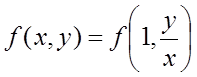 ,
,
тобто однорідна функція залежить
тільки від відношення ![]() . Рівняння (6) приймає вид:
. Рівняння (6) приймає вид:
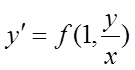 . (7)
. (7)
Уведемо
підстановку: 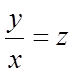 , у=хz, тоді
, у=хz, тоді ![]() або
або ![]() .
.
Підставляючи у і у' у рівняння (7), одержимо рівняння з розділюючимися перемінними:
![]() .
.
Розділимо перемінні:
![]()
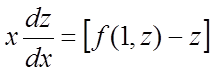
![]()
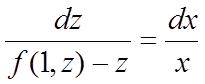 .
.
Інтегруючи, знайдемо:
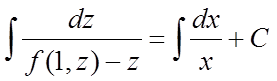 .
.
Підставляючи
після інтегрування замість z відношення ![]() ,
одержимо загальний інтеграл рівняння (7).
,
одержимо загальний інтеграл рівняння (7).
Наприклад:
вирішити рівняння ![]() .
.
Перепишемо
рівняння у виді: 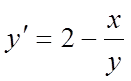 . Праворуч стоїть функція
. Праворуч стоїть функція  – нульового виміру. Дане рівняння є
однорідним першого порядку. Робимо заміну:
– нульового виміру. Дане рівняння є
однорідним першого порядку. Робимо заміну: 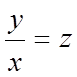 , у=хz,
, у=хz,
![]() , рівняння переписується
, рівняння переписується
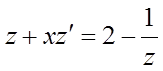 ,
,
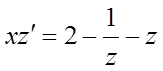
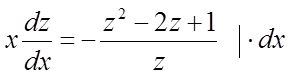
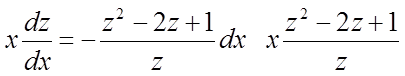
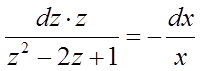 .
.
Інтегруючи, одержимо:
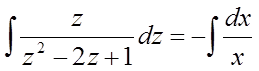 ,
,
перепишемо:
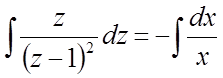 .
.
Віднімемо 1 і додамо 1 у чисельнику і почленно розділимо:
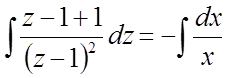
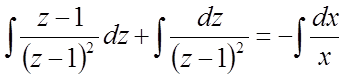 або
або 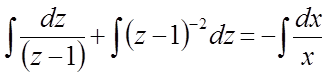 ,
,
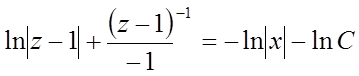 ,
,
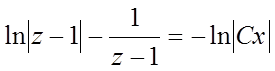 ,
,
підставляючи 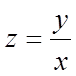 ,
запишемо загальний інтеграл рівняння:
,
запишемо загальний інтеграл рівняння:
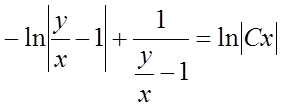 ,
,
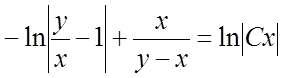 ,
, 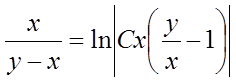 .
.
Зауваження: Рівняння виду ![]() називається однорідним, якщо функції
називається однорідним, якщо функції ![]() і
і ![]() є
однорідними функціями того самого виміру.
є
однорідними функціями того самого виміру.
Наприклад, рівняння:
![]() ,
,
![]() ,
,
![]()
є однорідними рівняннями.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.