Лекція 3
План.
1. Екстремум функції декількох перемінних.
2. Умовний экстремум. Найбільше і найменше значення функції в замкнутій області.
1. Екстремум функції декількох перемінних
Экстремум функції.
Функція ![]() має максимум (мінімум) у крапці
має максимум (мінімум) у крапці ![]() , якщо значення функції в цій крапці більше
(менше), чим її значення в будь-якій іншій крапці
, якщо значення функції в цій крапці більше
(менше), чим її значення в будь-якій іншій крапці ![]() деякої
околиці крапки
деякої
околиці крапки ![]() , тобто
, тобто ![]() [відповідно
[відповідно
![]() ] для всіх крапок
] для всіх крапок ![]() ,
що задовольняють умові
,
що задовольняють умові ![]() , де δ – досить
мале позитивне число.
, де δ – досить
мале позитивне число.
Максимум або
мінімум функції називається її экстремумом. Крапка ![]() , у якій функція має экстремум, називається
крапкою экстремума.
, у якій функція має экстремум, називається
крапкою экстремума.
Якщо
диференціюємо функція ![]() досягає экстремума в крапці
досягає экстремума в крапці ![]() , то
її приватні похідні першого порядку в цій крапці дорівнюють нулеві, тобто
, то
її приватні похідні першого порядку в цій крапці дорівнюють нулеві, тобто
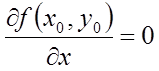 ,
, 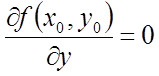
(необхідні умови экстремума).
Крапки, у яких приватні похідні дорівнюють нулеві, називаються стаціонарними крапками. Не всяка стаціонарна крапка є крапкою экстремума.
Нехай ![]() –
стаціонарна крапка функції
–
стаціонарна крапка функції ![]() . Позначимо
. Позначимо
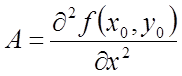 ,
, 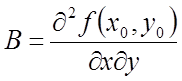 ,
, 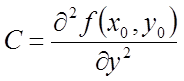
і складемо дискримінант ![]() .
Тоді:
.
Тоді:
якщо Δ > 0, то функція має в крапці
![]() экстремум, а саме максимум при А
< 0 (або З < 0) і мінімум при А > 0 (або З >
0);
экстремум, а саме максимум при А
< 0 (або З < 0) і мінімум при А > 0 (або З >
0);
якщо Δ < 0, то в крапці ![]() экстремума немає (достатні умови
наявності або відсутності экстремума);
экстремума немає (достатні умови
наявності або відсутності экстремума);
якщо Δ = 0, то потрібне подальше дослідження (сумнівний випадок).
Приклад 1.
Знайти экстремум функції ![]() .
.
Рішення. Знаходимо приватні похідні першого порядку:
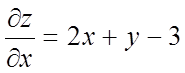 ,
, 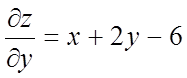 .
.
Скориставшись необхідними умовами экстремума, знаходимо стаціонарні крапки:
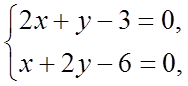
відкіля х = 0, у = 3; М (0; 3).
Знаходимо значення приватних похідних другого порядку в крапці М
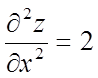 ,
, 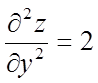 ,
, 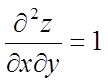
і складаємо дискримінант
![]() .
.
Отже, у крапці М (0; 3) задана
функція має мінімум. Значення функції в цій крапці ![]() .
.
Приклад 2.
Знайти экстремум функції
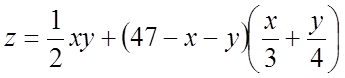 .
.
Рішення. Знаходимо приватні похідні першого порядку:
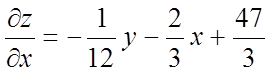 ,
, 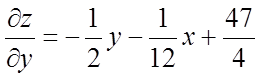 .
.
Скориставшись необхідними умовами экстремума, знаходимо стаціонарні крапки:
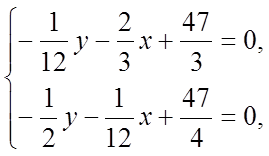 або
або 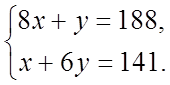
Звідси х =21, у = 20; стаціонарна крапка М (21; 20).
Знайдемо значення других похідних у крапці М:
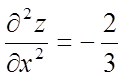 ,
, 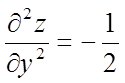 ,
, 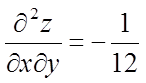 .
.
Тоді
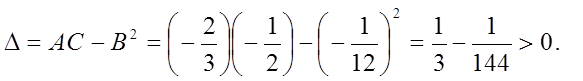
Тому що А < 0, то в крапці М
(21; 20) функція має максимум: ![]() .
.
2. Умовний экстремум. Найбільше і найменше значення функції в замкнутій області.
Умовним
экстремумом
функції ![]() називається экстремум цієї функції,
досягнутий за умови, що перемінні х и у зв'язані рівнянням
називається экстремум цієї функції,
досягнутий за умови, що перемінні х и у зв'язані рівнянням ![]() (рівняння зв'язку).
(рівняння зв'язку).
Відшукання умовного экстремума можна звести до дослідження на звичайний экстремум так називаної функції Лагранжа
![]() ,
,
де λ – невизначений постійний множник.
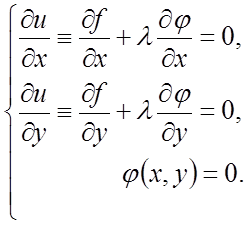
З цієї системи трьох рівнянь можна знайти невідомі х, у і λ.
Для того, щоб знайти найбільше і найменше значення функції в замкнутій області, треба:
1) знайти стаціонарні крапки, розташовані в даній області, і обчислити значення функції в цих крапках;
2) знайти найбільше і найменше значення функції на лініях, що утворять границю області;
3) їх усіх знайдених значень вибрати найбільше і найменше.
Приклад 1.
Знайти экстремум функції ![]() за умови, що х и у зв'язано
рівнянням
за умови, що х и у зв'язано
рівнянням ![]() .
.
Рішення.
Розглянемо функцію Лагранжа ![]() . Маємо
. Маємо 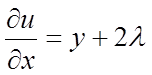 ,
, 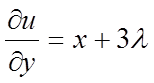 . Із
системи рівнянь (необхідні умови экстремума)
. Із
системи рівнянь (необхідні умови экстремума)
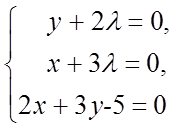
знаходимо, що λ = −5/12, х
= 5/4, у = 5/6. Неважко бачити, що в крапці (5/4; 5/6) функція ![]() досягає найбільшого значення
досягає найбільшого значення ![]() .
.
Приклад 2.
З усіх прямокутних трикутників із заданою площею S знайти такий, гіпотенуза якого має найменше значення.
Рішення. Нехай х
и у – катети, а z – гіпотенуза трикутника. Тому що ![]() , те задача зводиться до знаходження
найменшого значення функції
, те задача зводиться до знаходження
найменшого значення функції ![]() за умови, що х и
у зв'язано рівнянням
за умови, що х и
у зв'язано рівнянням ![]() , тобто
, тобто ![]() . Розглянемо функцію
. Розглянемо функцію ![]() і знайдемо її приватні похідні
і знайдемо її приватні похідні
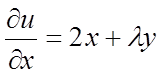 ,
, 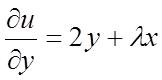 .
.
Тому що ![]() ,
, ![]() , то із системи рівнянь
, то із системи рівнянь
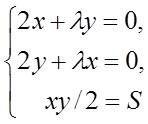
одержуємо рішення λ = −2, х = у =
![]() .
.
Таким чином, гіпотенуза має найменше значення, якщо катети трикутника рівні між собою.
Приклад 3.
Знайти найменше і
найбільше значення функції ![]() в колі
в колі ![]() .
.
Рішення. Тут
розглядається область D, обмежена окружністю ![]() ,
включаючи і крапки окружності.
,
включаючи і крапки окружності.
Знайдемо
стаціонарні крапки даної функції; маємо 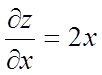 ,
, 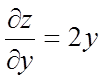 ; у силу необхідних умов экстремума
знаходимо, що х = 0, у = 0.
; у силу необхідних умов экстремума
знаходимо, що х = 0, у = 0.
Досліджуємо на умовний экстремум функцію ![]() , якщо х и у зв'язані
співвідношенням
, якщо х и у зв'язані
співвідношенням ![]() . Розглянемо функцію
. Розглянемо функцію
![]() .
.
Знаходимо приватні похідні
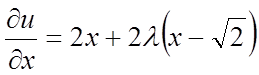 ,
, 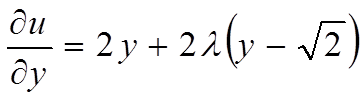 .
.
Для визначення х, у і λ одержуємо систему рівнянь
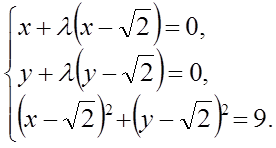
Ця система має два рішення: ![]() ,
,
![]() і
і ![]() ,
, ![]() і
і ![]() .
Виходить, найбільше значення функція приймає в крапці
.
Виходить, найбільше значення функція приймає в крапці ![]() .
.
Отже, ![]() ,
, ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.