Лекція 9
План:
9.1. Задача про роботу поля Земного тяжіння.
9.2. Задача про роботу сил електричного поля.
9.3. Задача про виділення тепла ідеальним газом.
9.4. Задача про кількість рідини, яка протікає через замкнутий контур.
9.5. Задача про роботу газу, який розширяється в циліндрі.
9.6. Задача про обчислення площі плоскої фігури.
9.7. Задача про обчислення площі циліндричної форми.
9.8. Приклади застосування криволінійних інтегралів.
9.9 Запитання для самоперевірки.
Українсько-російський словник вжитих в лекції слів, які в мовах мають різне звучання.
|
Задовольняють – – удовлетворяют Поверхово –поверхностно Однозв’язну –односвязную Шлях – путь Тяжіння – тяжесть Позитивна – положительная Негативна –отрицательная Звідки – отсюда Рух – движение Створеного – образованого Враховуючи – учитывая |
Речовина – вещество Вихідний стан –исходное состояние Ділянка – участок Часток –частиц Вироблену – –произведённую Виміру – измерения Відповідний – –соответствующий Істотно –существенно Усталений – – установившийся |
Визначену – определённую Підсумовуємо –суммируем Дотична –касательная Співпав –совпал Заздалегідь –заблаговременно Джерело – истосник Стоки –стоки Двигун –двигатель Прямувати – стремиться Зручна –удобная Нестислива – –несжимающаяся Швидкість –скорость |
Математичні факти з попередніх розділів, які використовуються в даній лекції.
1. Закон всесвітнього тяжіння 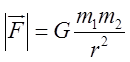 . Вага тіла, масою т, яке
знаходиться на земній поверхні, або сила з якою Земля притягає це тіло:
. Вага тіла, масою т, яке
знаходиться на земній поверхні, або сила з якою Земля притягає це тіло: ![]() .
.
2. Як дзеркальке відображення закону
всесвітнього тяжнння – закон Кулона про силу з якою взаємодіють два заряди ![]() , які знаходяться на віддалі
, які знаходяться на віддалі 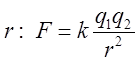 .
.
3. Теорема про величину зовнішнього кута трикутника.
|
|
Кут ACD=![]() з одного боку і в той же час
з одного боку і в той же час ![]() . Звідси маємо
. Звідси маємо ![]() , (*). Як відомо, сума внутрішніх кутів
трикутника дорівнює
, (*). Як відомо, сума внутрішніх кутів
трикутника дорівнює ![]() . Тому
. Тому ![]() .
Звідси маємо
.
Звідси маємо ![]() (**). Порівнюючи (*) і (**)
одержимо
(**). Порівнюючи (*) і (**)
одержимо ![]() . Зовнішній кут трикутника дорівнює сумі
двох внутрішніх не суміжних з ним.
. Зовнішній кут трикутника дорівнює сумі
двох внутрішніх не суміжних з ним.
4. Об’єм циліндра, радіусом R і висотою H ![]() .
.
5.![]() .
. ![]() .
.
6. Слід памятати, що радіус вектор точки ![]() – це вектор, який сполучає початок
координат, тобто точку
– це вектор, який сполучає початок
координат, тобто точку ![]() з точкою М. Довжина його завжди
з точкою М. Довжина його завжди 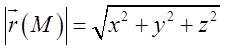 очевидно, що довжина є функцією координат
точки М. Одиничний вектор
очевидно, що довжина є функцією координат
точки М. Одиничний вектор ![]() має такі координати
має такі координати 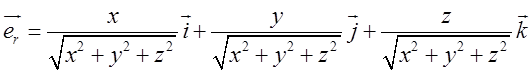 , або
, або ![]() , де
, де ![]() кути між радіус-вектором і відповідними
вісями.
кути між радіус-вектором і відповідними
вісями.
7. Площа трикутника заданого своїми трьома
вершинами ![]() знаходиться за формулою
знаходиться за формулою 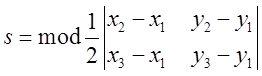 , яка є наслідком геометричного змісту
векторного добутку.
, яка є наслідком геометричного змісту
векторного добутку.
9.1. Задача про роботу поля Земного тяжіння
Сьому лекцію ми
починали з задач, які приводять до поняття криволінійних інтегралів.
Повернемось знову до задачі про роботу силового поля,
заданого своїми функціями-проекціями на координатні вісі ![]()
Якщо функції-проекції сили ![]() на осі координат задовольняють умовам
на осі координат задовольняють умовам 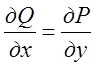 ;
;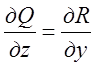 ;
;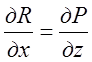 і поле займає поверхово
однозв'язну область, то робота в
цьому силовому полі, яка виражається криволінійним інтегралом
і поле займає поверхово
однозв'язну область, то робота в
цьому силовому полі, яка виражається криволінійним інтегралом 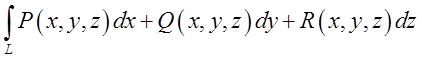 , не
залежить від форми шляху. Таке силове поле називається потенціальним чи консервативним.
Функція
, не
залежить від форми шляху. Таке силове поле називається потенціальним чи консервативним.
Функція ![]() , для якої вираз
, для якої вираз ![]() є повним
диференціалом, називається потенціалом силового поля.
Згідно з результатами одержаними вище, можна сказати, що робота
в потенціальному силовому полі дорівнює різниці
потенціалів: потенціал від кінечної точки шляху минус потенціал від початкової точки шляху.
є повним
диференціалом, називається потенціалом силового поля.
Згідно з результатами одержаними вище, можна сказати, що робота
в потенціальному силовому полі дорівнює різниці
потенціалів: потенціал від кінечної точки шляху минус потенціал від початкової точки шляху.
Як приклад,
розглянемо поле Земного тяжіння. Наша
задача: знайти потенціал цього поля. Для
розв’язку виберемо в площині руху матеріальної точки маси т координатні осі, причому вісь Оу
направимо вертикально вниз, осі Ох і Oz будуть паралельні Земній поверхні, а тому проекції сили ваги на
осі координат будуть такі: ![]() .
Робота при переміщенні матеріальної точки з точки
.
Робота при переміщенні матеріальної точки з точки ![]() у
точку
у
точку ![]() виразиться інтегралом
виразиться інтегралом 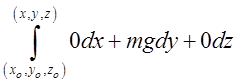 =
= .
(9.1)
.
(9.1)
Ця робота
позитивна, якщо ![]() , тобто якщо матеріальна точка падає, негативна, якщо точка піднімається
і дорівнює 0, якщо точка, описавши яку завгодно траєкторію, опинеться на тій же
висоті, звідки вона починала свій рух тобто
, тобто якщо матеріальна точка падає, негативна, якщо точка піднімається
і дорівнює 0, якщо точка, описавши яку завгодно траєкторію, опинеться на тій же
висоті, звідки вона починала свій рух тобто![]() . Як видно з обчислення, потенційна функція
. Як видно з обчислення, потенційна функція ![]() залежить лише від однієї
змінної імає вид
залежить лише від однієї
змінної імає вид ![]() . Звичайно довільну постійну С вибирають
так, щоб
. Звичайно довільну постійну С вибирають
так, щоб ![]()
при у= 0. Тоді потенціалом поля тяжіння буде функція
![]() .
.
9.2. Задача про роботу сил електричного поля
|
|
Наступним прикладом візьмемо електричне поле створюване точковим зарядом. У початок координат помістили точковий заряд +q. Визначити потенціал створеного зарядом поля.
Для
розвязку цієї задачі обчислимо силу з якою цей заряд +q діє на пробний одиничний позитивний
заряд, поміщений у точку М(x,y,z). Величина цієї сили визначиться за законом
. Кулона: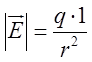 , де r віддаль від заряду q до одиничного
заряду – Рис.9.1 (або до точки
, де r віддаль від заряду q до одиничного
заряду – Рис.9.1 (або до точки ![]() ), а тому
), а тому ![]() .
Обчислимо проекції сили
.
Обчислимо проекції сили ![]() на координатні вісі
(див. Рис.9.1 враховуючи, що
на координатні вісі
(див. Рис.9.1 враховуючи, що 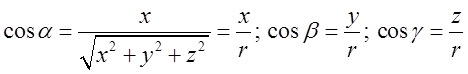 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.