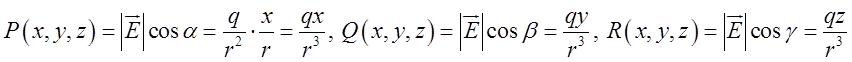Застосування криволінійних інтегралів, страница 2

   . Поле описується такою вектор-функцією 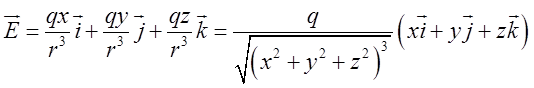.  Перевіримо потенціальність, тобто виконання рівностей 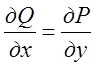 ,,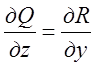, 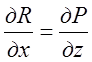враховуючи, що;   ;.

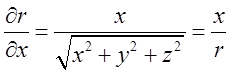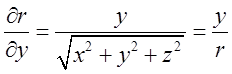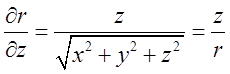Тоді 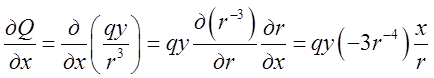, аналогічно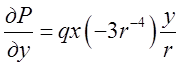   

і, як бачимо, 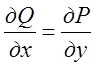. Інші дві рівності також виконуються – перевірте самостійно. Поле потенціальне. Робота не залежить від форми шляху інтегрування. = =

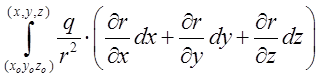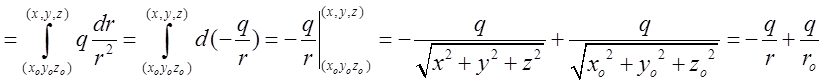 . (9.2)  Так, як величина  є величина постійна,  то потенціалом поля є функція 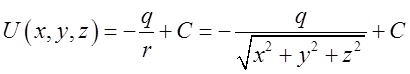                                                                                  (9.3)

Тому, що заряди однойменні, то робота позитивна при їхньому віддаленні друг від друга  і негативна при їхньому зближенні .

9.3. Задача про  виділення тепла ідеальним газом. Ентропія

Перш ніж поставити задачу визначимось з термінологією та поняттями, які застосовуються в термодінаміці. Будемо під станом речовини розуміти сукупність величин, що характеризують її фізичний стан. У термодинаміці звичайно цими величинами служать: тиск – р, об’єм – v  і абсолютна температура – Т. Отже, стан визначається трьома величинами: р, v, Т. Але вони зв'язані між собою одним рівнянням – так званим рівнянням стану. Тому стан фактично визначається двома величинами, наприклад р i v (третя, Т, є функція р i v).   При подальшому досліджені виділення тепла, за осі системи координат ми візьмемо р і v.   Геометрично кожному стану відповідає точка М (р,v) у площині РOV, а кожному процесу ( що складається в послідовній зміні стану тіла) – лінія. Вона називається діаграмою процесу. У тому випадку, коли відбувається повернення до вихідного стану, процес називають круговим чи циклічним;  (згадайте зі школи – цикл Карно) його діаграмою будe замкнута линия.

Нехай маємо ідеальний газ, тобто газ, в якому виконується рівняння стану Менделеєва – Клапейрона  , де R універсальна газова постійна величина.

Поставимо перед собою задачу – знайти кількість тепла Q, поглиненого (чи виділеного) газом при процесі, зображеному даною діаграмою L. На кривій циклу L виділимо довільну її ділянку від точки М(р,v) до точки   і розглянемо «нескінченно малий» процес. Кількість тепла, яка виділиться під час цього процесу, позначимо через .  Згідно першому закону термодинаміки це тепло йде на збільшення внутрішньої енергії часток газу, тобто у кінцевому рахунку на збільшення  температури газу, і на роботу, вироблену при зміні об’єму . Ми знайдемо елемент  (головну  частину , лінійну відносно  и ), якщо допустимо, що  поглинуте тепло є сума двох кількостей тепла: 1) того, яке пішло на збільшення температури  при постійному об’ємі v; 2) витраченого на роботу розширення  при постійній температурі Т.  Перше дорівнює   — теплоємність газу при постійному об’ємі, а друге .

Отже, при відповідному виборі одиниць виміру  (*).

Символ  введений тому, що, як стане ясно з подальшого, ця величина не є повним диференціалом. Відповідно до рівняння Менделеева – Клапейрона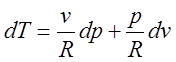

вносячи це у вираз (*), після перегрупіровки одержимо  .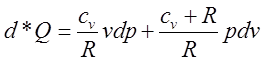

З'ясуємо зміст вирау . З двох останніх формул при постійному тиску р, а це значить, що , знаходимо 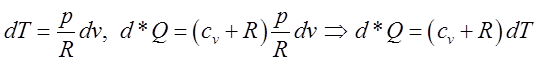, звідки видно, що коефіцієнт при   є просто теплоемність  при постійному тиску: (**)

А тому остаточно запишемо 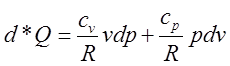. Це і буде елементарна зміна кількості тепла, а для того, щоб знайти зміну  всього тепла, при зміні стану газу вздовж L треба проінтегрувати цей вираз  по кривій L, яка є діаграмою процесу.

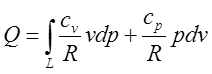                                                                        (9.4)

Це є відповідь на поставлене питання задачі, але досліджуючи цей розв’язок, ми  одержимо ще деякі цікаві результати. В (9.4) умови незалежності інтеграла від шляху інтегрування не виконуються.  Дійсно, 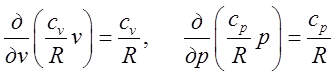  і так, як , то 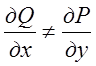 (ось чому писали).