Як ми знаємо з попередньої лекції, значення криволінійного інтегралу від повного диференціалу не залежить від шляху інтегрування, а залежить лише від координат початкової і кінцевої точок інтегрування, тому
Рис.9.8.
шлях інтегрування обираємо довільно. Нам найвигідніше інтегрувати вздовж
ламаної лінії, кожна із ланок якої буде паралельна одній з осей координат. На
рисунку це ОАВС. Тоді 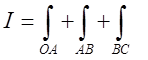 .
.
На відрізку ОА
змінюється лише х ; ![]() , тому
, тому 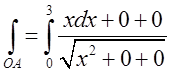 . На відрізку АВ змінюється лише у;
. На відрізку АВ змінюється лише у; ![]() , тому
, тому 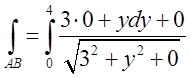 . На
відрізку ВС змінюється лише z;
. На
відрізку ВС змінюється лише z; ![]() , тому
, тому 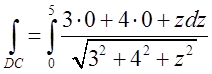 . Підставивши знайдені інтегрили остаточно
одержимо
. Підставивши знайдені інтегрили остаточно
одержимо 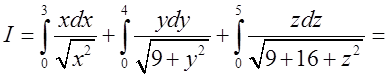
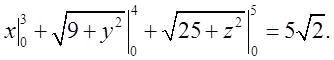 Це і є відповідь.
Це і є відповідь.
П.4. Знайти первісну функцію за її повним диференціалом ![]() .
.
Розвязок. Для того,
щоб знайти первісну функції за її повним диференціалом проінтегруємо повний
диференціал від якої-небудь конкретної точки, наприклад від ![]() , до поточної точки
, до поточної точки ![]() .
.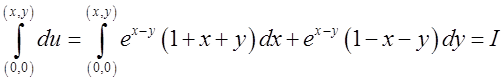 . Інтегруємо вздовж ламаної
. Інтегруємо вздовж ламаної ![]() , де В(х,0) .
, де В(х,0) . ![]() . На відрізку
. На відрізку ![]() змінюється
лише х;
змінюється
лише х; ![]() . На відрізку ВМ змінюється лише у;
. На відрізку ВМ змінюється лише у; ![]() . Враховуючи це матимемо:
. Враховуючи це матимемо: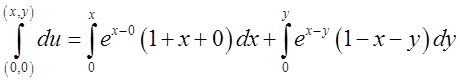 .
. 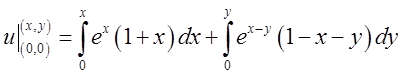 .
Інтегруючи обидва інтеграли частинами одержимо
.
Інтегруючи обидва інтеграли частинами одержимо ![]() . Після
очевидних перетворень прийдемо до рівності
. Після
очевидних перетворень прийдемо до рівності ![]() .
Значення функції
.
Значення функції ![]() , тому остаточно
, тому остаточно ![]() .Тобто за повним диференціалом функції ми
можемо відновити її лише з тосністю до постійної величини.
.Тобто за повним диференціалом функції ми
можемо відновити її лише з тосністю до постійної величини.
П.5. Знайти масу першого витка гвинтової лінії![]() , якщо
лінійна густина цієї лінії в кожній її точці дорівнює радіус-вектору цієї
точки.
, якщо
лінійна густина цієї лінії в кожній її точці дорівнює радіус-вектору цієї
точки.
Розв’язок: 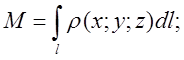 знайдемо
знайдемо![]()
![]() .
Очевидно, що
.
Очевидно, що ![]()
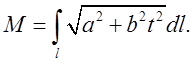 Знайдемо
Знайдемо 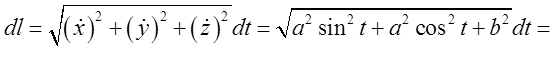
![]()
![]()
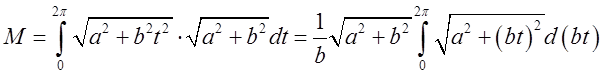 = =
= =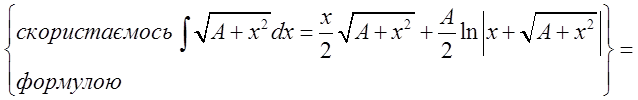
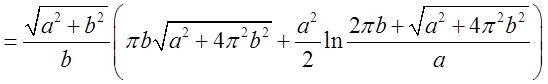
одиниць маси. Це і є відповідь.
П.6. Знайти момент інерції відносно осі z першого витка гвинтової лінії ![]() .
.
Розв’язок. Використаємо формулу ![]() , де r – відстань від маси
, де r – відстань від маси ![]() до осі l. Tак як відстань до осі 0Z
у гвинтової лінії постійна і дорівнює
до осі l. Tак як відстань до осі 0Z
у гвинтової лінії постійна і дорівнює ![]() ,то
,то
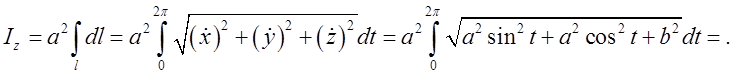
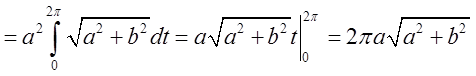 . Це і є відповідь.
. Це і є відповідь.
П.7. Маса М розподілена рівномірно (з постійною густиною) вздовж кола 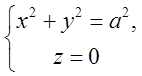 .Визначити силу, з якою ця маса діє на масу
т , розміщену в точці
.Визначити силу, з якою ця маса діє на масу
т , розміщену в точці ![]() .
.
|
|
Розв’язок.
Визначимо функцію лінійної густтини маси на колі: 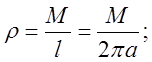 так,
як довжина кола дорівнює
так,
як довжина кола дорівнює ![]() . Візьмемо елементарний
відрізок довжини кола
. Візьмемо елементарний
відрізок довжини кола 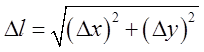 і визначимо силу, з якою дуга
маси
і визначимо силу, з якою дуга
маси 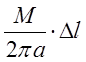 діє на масу т . Згідно
закону Ньютона величина цієї сили
діє на масу т . Згідно
закону Ньютона величина цієї сили ![]() буде:
буде: 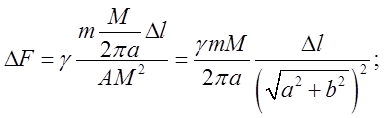 протилежний відрізок
протилежний відрізок ![]() діє на точку точно з такою ж за величиною
силою
діє на точку точно з такою ж за величиною
силою ![]() . Сума двох векторів сил
. Сума двох векторів сил ![]() – буде направлена вздовж осі 0Z і по абсолютній величині дорівнює
– буде направлена вздовж осі 0Z і по абсолютній величині дорівнює ![]() . Так як
. Так як 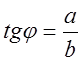 , а
, а 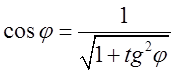 , то
, то 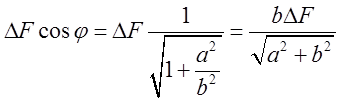 .
Нехай
.
Нехай ![]()
![]()
![]() ,
тоді маємо
,
тоді маємо 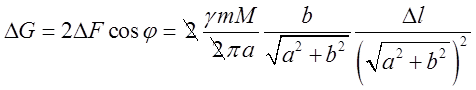
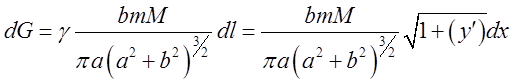 , якщо рівняння кола
задано в параметричній формі
, якщо рівняння кола
задано в параметричній формі ![]()
![]() , то
, то 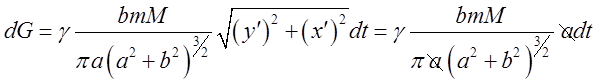 .
Проінтегрувавши від 0 до
.
Проінтегрувавши від 0 до ![]() одержимо
одержимо 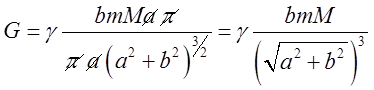 . Відповідь:
. Відповідь: 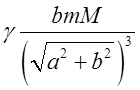 Н.
Н.
Запитання для самоперевірки.
1.
Чому дорівнює робота сил поля Земного тяжіння при
переміщенні маси т з висоти h на висоту H? Розгляньте випадок коли ![]() .
.
2. Які поля ми називаємо потенціальними?
3. Що ми називаємо потенціалом силового поля? Як його знайти?
4. Чому дорівнює потенціал силового поля утвореного електричним зарядом q?
5. Що характеризує ентропія?
6.
Чому дорівнює кількість рідини, яка проходить через
криву L, якщо швидкість рідини ![]() ?
?
7. Чому дорівнює кількість рідини, яка проходить через замкнутий контур L?
8. Як знаходять роботу газу, який розширюючись рухає поршень?
9.
Як обчислити площу плоскої фігури обмеженої
замкнутим контуром![]() ?
?
10. Як обчислити площу циліндричної поверхні?
11. Яке інше (крім маси кривої) можна дати тлумачення криволінійному інтегралу І-го типу?
Розвязати самостійно.
9.1. Поле утворене
силою, яка направлена паралельно вісі у в протилежну їй сторону по
величині рівною абсцисі точки прикладення. Знайти роботу сили поля при
переміщенні маси т по параболі ![]() від
точки А(1;0) до точки В(0;1). Відп.-8т/15.
від
точки А(1;0) до точки В(0;1). Відп.-8т/15.
9.2. Поле утворене силою F=k/r ,
направленою перпендикулярно до радіуса-вектора![]() точки
прикладення. Знайти роботу поля при переміщенні матеріальної точки масою т
по дузі першої чверті кола
точки
прикладення. Знайти роботу поля при переміщенні матеріальної точки масою т
по дузі першої чверті кола ![]() із точки А(а;0)
в точку В(0;а). Відп.
із точки А(а;0)
в точку В(0;а). Відп. ![]() .
.
9.3. Знайти масу
дільниці ланцюгової лінії 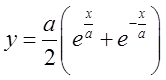 між точками х=0 і
х=а, якщо густина кривої
між точками х=0 і
х=а, якщо густина кривої 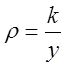 . Відп.
. Відп. ![]()
9.4. Обчислити
площу кардіоїди: ![]() . Відп.
. Відп.![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.