S=![]() -
-![]() =
=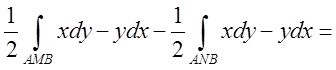
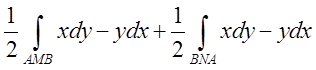 .
.
Але ж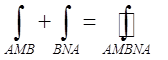 , а тому
, а тому 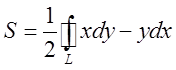 (9.8)
(9.8)
Ця формула найбільш зручна для обчислення площ плоских фігур.
9.7. Задача про обчислення площі циліндричної поверхні
|
|
Дана циліндрична поверхня G. Її напрямною в площині хОу служить крива L, задана від точки А до точки В. Твірні
циліндричної поверхні паралельні осі z. Обчислити площу Q
циліндричної поверхні, яка обмежена кривою L знизу та іншою кривою ![]() зверху,
аплікати якої є функції координат точки Р, яка лежить на лінії L:
зверху,
аплікати якої є функції координат точки Р, яка лежить на лінії L: ![]() .
.
При
уважному аналізі умови задачі, помічаємо, що ця задача абсолютно рівносильна
задачі (розв’язаній в лекції 7) про знаходження маси кривої з лінійною густиною
![]() . Рис. 9.5. Розвязуємо
її за допомогою таких же міркувань як і при розв’язанні
задачі про масу. На кривій L в
довільній точці Р(х,у) виділимо
елемент дуги
. Рис. 9.5. Розвязуємо
її за допомогою таких же міркувань як і при розв’язанні
задачі про масу. На кривій L в
довільній точці Р(х,у) виділимо
елемент дуги ![]() рис. 9.5. Цьому елементу дуги відповідає
площа циліндричної поверхні (на рисунку заштрихована). Ця площа
рис. 9.5. Цьому елементу дуги відповідає
площа циліндричної поверхні (на рисунку заштрихована). Ця площа ![]() приблизно дорівнює
площі прямокутника у якого основа
приблизно дорівнює
площі прямокутника у якого основа ![]() , а висота f(x,y), тобто
, а висота f(x,y), тобто ![]() . Щоб знайти площу
всієї поверхні треба цю рівність проінтегрувати вздовж кривої L від точки А до точки В, або навпаки
. Щоб знайти площу
всієї поверхні треба цю рівність проінтегрувати вздовж кривої L від точки А до точки В, або навпаки
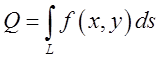 (9.9)
(9.9)
Осмислюючи
останню задачу і її розв’язок (9.9), ми можемо дати ще одне геометричне
тлумачення криволінійного інтегралу першого типу: якщо плоска крива L є основою тину або огорожі (по російські –
забору), а![]() буде висотою цього тину, то (9.9) виражає
площу поверхні цього вриволінійного тину зі змінною висотою.
буде висотою цього тину, то (9.9) виражає
площу поверхні цього вриволінійного тину зі змінною висотою.
В деяких випадках застосування (9.9) при обчислені площі поверхнні буває набагато раціональнішим, ніж застосування подвійних чи поверхневих інтегралів. Покажемо це на нступному прикладі 1.
9. 8. Приклади застосування криволінійних інтегралів
для конкретно поставлених задач
П.1. Обчислити площу поверхні, яку вирізає із круглого циліндра радіуса R такий же циліндр, якщо вісі цих циліндрів перетинаються під прямим кутом.
Розв’язок. Побудуємо фігуру перетину в декартовій прямокутній системі
координат . Вісі циліндрів направимо одну вздовж осі х, другу – вздовж
у . На рис.9.6 зображені півциліндри і четверта частина DABC всієї шуканої
поверхні. Тіло ж яке утворюють в перетині два ціліндри, матиме площу поверхні
вдвічі бвльшу (поверхня яку вирізає перший циліндр з другого плюс поверхня, яку
вирізає другий циліндр з першого). Це тіло буде симетричним відносно всіх
координатних площин, площин ![]() , всіх координатних
осей. Рівняння циліндрів будуть
, всіх координатних
осей. Рівняння циліндрів будуть ![]() . Розвязуючи цю систему
при z=0, одержимо
. Розвязуючи цю систему
при z=0, одержимо ![]()
![]() . Це ми одержали
рівняння проекцій ребер нашої фігури на площину хОу. Обчислимо площу поверхні ADB, взявши за лінію L криву BD, рівняння якої
. Це ми одержали
рівняння проекцій ребер нашої фігури на площину хОу. Обчислимо площу поверхні ADB, взявши за лінію L криву BD, рівняння якої
![]() , Рис.9.6.
або ввівши параметр-кут
, Рис.9.6.
або ввівши параметр-кут ![]() . Підінтегральною
функцією для формули (9.9) буде х=у. Диференціал дуги буде
. Підінтегральною
функцією для формули (9.9) буде х=у. Диференціал дуги буде 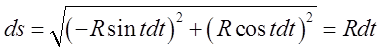 .
.
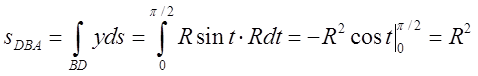 . Вся площа буде в вісім раз більшою.
. Вся площа буде в вісім раз більшою.
Відповідь.![]() (застосування подвійного інтегралу вимагає
вдвічі більшої роботи)
(застосування подвійного інтегралу вимагає
вдвічі більшої роботи)
|
|
|
Рис 9.6. Рис. 9.7
П.2. Обчислити 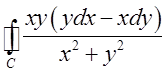 , де контур С права пелюстка
лемніскати Бернулі
, де контур С права пелюстка
лемніскати Бернулі ![]() .
.
Розвязок. Сумістимо
прямокутну і полярну системи координат. Побудуємо лемніскату Бернулі, надаючи
значень ![]() через кожні
через кожні ![]() і на
променях відкладаючи значення
і на
променях відкладаючи значення ![]() . Рис. 9.7.
. Рис. 9.7.![]() . Враховуючи парність косинуса, робимо
висновок, що полярна вісь, а значить і вісь Ох, буде для кривої віссю симетрії.
. Враховуючи парність косинуса, робимо
висновок, що полярна вісь, а значить і вісь Ох, буде для кривої віссю симетрії.
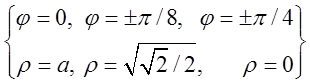 . При подальшому збільшені кута до
. При подальшому збільшені кута до ![]() буде
буде ![]() , і
вираз втрачає сенс. Тому права пелюстка лемніскати утвориться при
, і
вираз втрачає сенс. Тому права пелюстка лемніскати утвориться при ![]() . Це і будуть границі інтегрування.
Підставимо в умову
. Це і будуть границі інтегрування.
Підставимо в умову 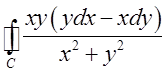 =
= 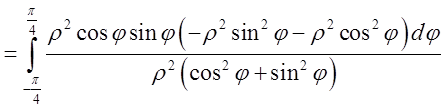 =
=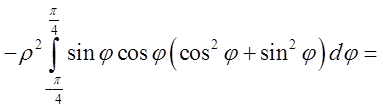
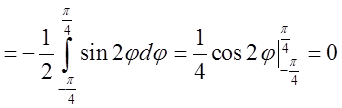 . Це і є відповідь.
. Це і є відповідь.
П.3. Обчислити криволінійний інтеграл від повного диференціала 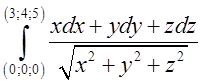 .
.
|
|
Розвязок. Очевидно,
що функція від якої взято повний диференціал має вид ![]() так,
як
так,
як 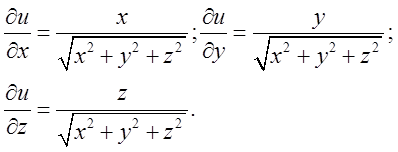
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.