Застосування криволінійних інтегралів, страница 3

            Таким чином, величина Q  істотно залежить від контуру L, тобто Q залежить не лише від р і v. Наше міркування показує, що кількість тепла, що поглинається (виділяється) не є функція стану газу, вона залежить не тільки від кінцевого стану, але і від того, яким способом газ прийшов до цьому стану, іншими словами, від сукупності всіх проміжних станів. Зокрема, круговий процес (цикл) може привести до  поглинання чи до виділення тепла. У термодинаміку уводиться величина S, що характеризує процес. Ця величина названа ентропією. Визначається ентропія інтегралом 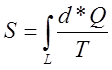 , де L –  діаграма процесу. Вираз 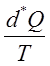 фізично означає величину зміни кількості виділеного тепла, яка припадає на один градус його температури.  Для ідеального газу знаходимо 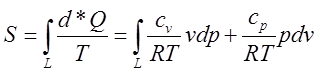. Так, як , то 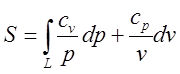 .  Підінтегральний вираз тепер уже є повний диференціал, тому що  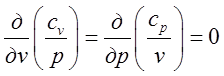. Значить величина інтегралу не залежить від форми шляху інтегрування, а залежить лише від координат кінцевої і початкової точки інтегрування. А це говорить про те, що ентропія є функцією стану газу; її величина не залежить від того, як газ змінюється від початкового стану до кінцевого. Інтегруючи, одержуємо

=

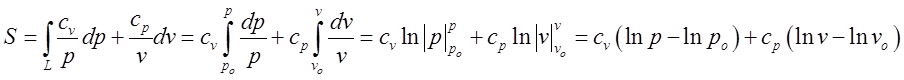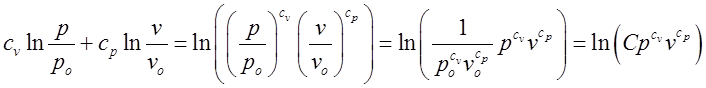=                        (9.5)

Якщо процес адіабатичний (то і ) тоді 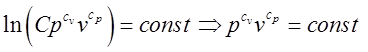, або перетворивши

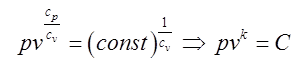,                                                                    (9.6)

де 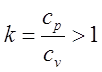. Рівняння (9.6) Вам знайоме з шкільного курсу фізики. Тепер ми подали його виведення. Це рівняння називається рівнянням  діаграми адіабатичного процесу (так званої адіабати) в ідеальному газі.

9.4. Задача про кількість рідини, яка протікає через замкнутий контур

Розглянемо плоский усталений рух нестисливої рідини. Такий рух характеризується тим, що, по-перше, усі її частинки, що лежать на одній вертикалі до деякої площини, мають ту саму швидкість так, що для характеристики всього руху досить вивчити рух в одній лише площині  і, по-друге,                         Рис.9.2                                                       швидкість частинки

 рідини залежить тільки від положення частинки, але не від часу. Таким чином, з кожною геометричною точкою розглянутої площини (чи її частини) зв'язана визначена по величині і напрямку швидкість; іншими словами, задане деяке «поле швидкостей», а це значить, що ми можемо застосувати висновки з лекції 7, замінивши знаходження кількості роботи на знаходження кількості рідини.

Позначимо   кут,   утворений   вектором   із з віссю  х, через , а проекції   цього вектора на координатні осі — через и і v, то (рис. 9.2, а) для проекцій очевидно одержимо

               (*)

Візьмемо тепер у площині  хОу яку-небудь криву (К) і постараємося визначити кількість Q рідини, що протікає через неї у визначену  сторону (як показано на рис.9.2 б) в одиницю часу. Припускаючи рідину нестисливої, можна кількість рідини вимірювати площею покритої нею фігури. Якщо фактично рідина тече в бік, протилежний обраному, то кількість рідини, що протікає, будемо вважати величиною від’ємною.Якщо вектор швидкості утворює не прямий кут з дотичною до кривої, то через криву рідина тече з швидкістю , де  – є проекція вектора  на нормаль до кривої К.

Розглянемо   елемент  MN=ds кривої (K). За час dt через цей елемент протече кількость рідини, рівна  с_п ds dt    (*),  де с_п є проекція швидкості на нормаль п до елемента ds, направлена у  вибрану нами сторону від кривої. Дійсно, ця кількість дорівнює площі паралелограма зі сторонами ds і сdt, висотою якого саме і є добуток c_ndt (рис. 9.2.б). Для підрахунку кількості рідини, що протікає через елемент ds в одиницю часу, підсумовуємо вираз (*) по елементах dt, що дасть c_nds – величина кількості рідини, що пройде через за деякий час Т=1.Підсумовуючи ж знайдені вирази по всіх елементах кривої (К), ми представимо шукану кількість Q рідини у виді криволінійного інтегралу першого типу 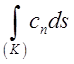                                                                                        (9.6).