Тригонометричні ряди Фур’є. Комплексна форма запису ряду Фур’є. Спектральна функція

Лекція 3

Тригонометричні ряди Фур’є

План:

 3.1. Тригонометричні ряди Фур’є.

 3.2. Комплексна форма запису ряду Фур’є.

 3.3. Представлення функції интегралом Фур’є.

 3.4. Найпростіші достатні умови зображення функції інтеграло Фур’є.

 3.5. Інтеграл Фур’є для парних функцій.

 3.6. Інтеграл Фур’є для непарних функцій.

 3.7. Комплексна форма інтегралу Фур’є.

 3.8. Поняття про перетворення Фур’є.

 3.9. Косинус – перетворення Фур’є.

 3.10. Синус – перетворення Фур’є.

 3.11. Спектральна функція.

 3.12. Запитання для самоперевірки.

Українсько-російський словник вжитих в лекції слів, які в мовах мають різне звучання.

Обмежена – ограниченная Парна –         чётная Непарна –    нечётная Складатися – состоять

Відповідно –     – соответственно Продовжили – продлили Переконаємось –        – убедимся

Спряжені – сопряжённые Поєднуючи – объединяя

Математичні факти з попередніх розділів, які використовуються в даній лекції.

1.Пригадаймо визначення синуса і косинуса: синус це відношення протилежного катета до гіпотенузи або проекція радіус-вектора одиничного кола на вісь Оу, а косинус це відношення прилеглого катета до гіпотенузи або проекція радіус-вектора одиничного кола на вісь Ох. Важливо пам’ятати, що при всіх  

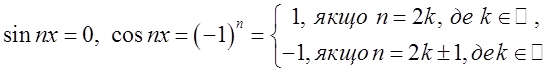
2. Інтегрування добутків  проводиться частинами за формулою 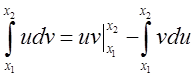, причому, якщо а=1 частинами інтегрують один раз, якщо а=2 – двічі, якщо а=к – к раз.

3.Інтегрування добутків  та  проводиться перетворенням цих добутків в суми за формулами 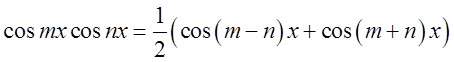 та .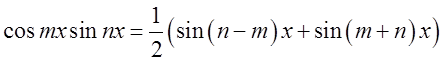

4. Невластиві інтеграли типу 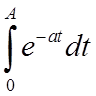 обчислюються так: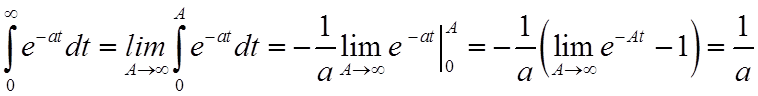

3.1.Тригонометричні ряди Фур’є. Теорема Діріхлє

Пригадаємо, як в аналітичній геометрії який-завгодно вектор  на площині хОу ми розкладали за двома перпендикулярними векторами , причому . Цей розклад мав вигляд: , де х і у  деякі  числові коефіцієнти, які ми назвали координатами вектора. Аналогічно в просторі який-завгодно вектор   ми розкладали за трьома взаємно перпендикулярними векторами , причому . Виникає питання: а чи не можна знайти сукупність (три, пять, чи більше) таких взаємно перпендикулярних функцій, щоб за ними можна було розкласти інші, які-завгодно (звичайно з певними обмеженнями) функції? Відповідь на це запитання позитивна. Такі функції єсть. Але треба визначитись в поняттях – ортогональність (перпендикулярність) і довжина. Для функцій ці поняття вводять слідуючим чином:

О. Система функцій  називається ортогональною в інтервалі , якщо інтеграл від добутку двох різних функцій системи дорівнює нулю: .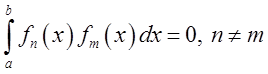

Квадрат довжини функції  (  називають нормою) визначають так: 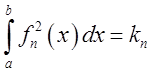. Якщо тепер кожну із системи ортогональних функцій розділимо на її норму, то одержимо ортонормовану (функції попарно взаємно перпендикулярні і кожна з них має одиничну довжину) систему функцій 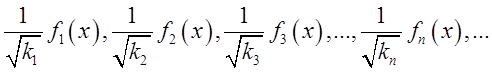 бо кожні дві з них залишилися перпендикулярними і тепер уже 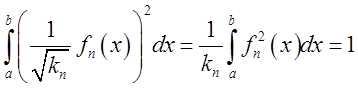. Безпосередньою перевіркою можна переконатися, що система функцій 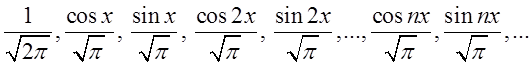є ортонормованою на проміжку , а значить , задану на цьому проміжку, можна розкласти за цією системою: 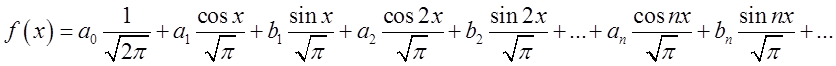.Щоб знайти коефіцієнти  досить домножити обидві частини вищенаписаної рівності на 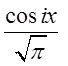або  на  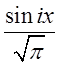 і проінтегрувати. Так наприклад щоб знайти  домножимо обидві частини  рівності на 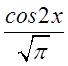 і проінтегруємо. 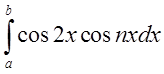Так як система функцій ортогональна, то при  всі інтеграли  і 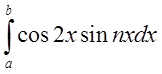  дорівнюють нулеві і залишиться тільки 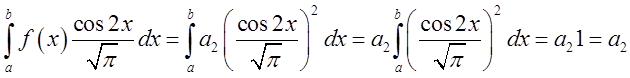. Аналогічно ми можнмо знайти який-завгодно коефіцієнт. А тому сформулюємо наступне твердження.

Нехай функцію  задано на проміжку , тоді цю функцію можна розвинути в тригонометричний ряд, який має назву ряд Фур’є і має такий вид: 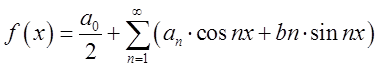   ;                                                                       (3.1)

де коефіцієнти  обчислюють за формулами:

;   ;

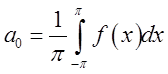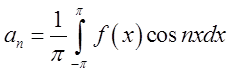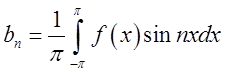 ; при чому                                                                   (3.2)

Теорема Діріхлє про розвинення  функції в ряд Фур’є

Якщо функція на інтервалі ; є  1) кусочномонотонна;

2) кусочнонеперервна; 3) обмежена то її  тригонометричний ряд Фур’є збігається в усіх точках сегмента . Якщо  – сума тригонометричного ряду Фур’є функції  , то в усіх точках неперервності цієї функції , а в усіх точках розриву 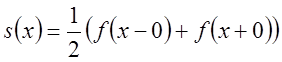. Крім того  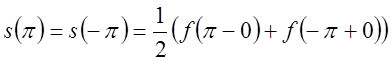     (3.3)

            Велике практичне застосування в електронній техніці набули генератори, які створюють періодичні імпульси з заданою частотою і заданою конфігурацією – як правило прямокутною або трикутною (пилкоподібною). Нижче ми представимо такі імпульси в вигляді рядів Фур’є і простежимо, яким чином графік функції імпульса наближено одержується з графіків послідовних частинних сум ряду Фур’є.

П.1. Розвинемо в ряд прямокутний імпульс заданий в інтервалі  так: 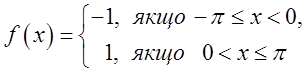 В точці х=0 імпульс переривається, тобто ця точка є точкою розриву функції.

Розв’язок. Так задана функція задоаольняє умови теореми Діріхлє і оскільки вона непарна, то .

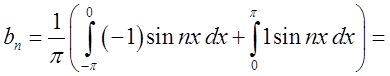
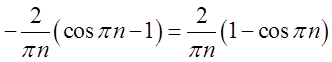. Так як  , то 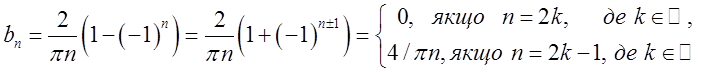 Розвинення заданої функції в ряд Фур’є має вигляд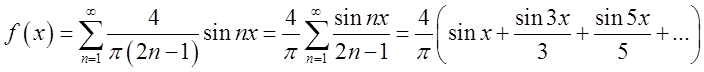

На цьому прикладі наглядно видно виконання теореми Діріхлє. А й справді: при х=0 та  сума ряду 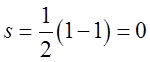. Використовуючи  рис.3.1, простежимо, яким чином графік функції імпульса наближено одержується з графіків послідовних частинних сум ряду Фур’є. На рис.3.1.а добре видно, що 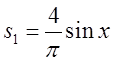 дорівнює 0 в точках  і віддалено наближує графік вихідної функції в решті точок. Але наступна частиння сума 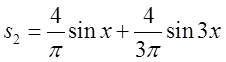,  на рис.3.1.б це суцільна крива лінія, яка по чотири рази перетинає кожен з відрізків імпульса, зберігаючи нульові значення в точках , вже набагато точніше 

                            Рис.3.1.                               наближує графік вихідної функції в решті точок.