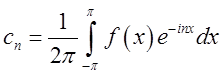Тригонометричні ряди Фур’є. Комплексна форма запису ряду Фур’є. Спектральна функція, страница 3

                                                                                    (3.12)

Якщо функція   дійсна ( а дотепер ми тільки такі функції і розглядали), то з формул (3.11) випливає, що коефіцієнти  розвинення в комплексний ряд Фур'є є комплексними спряженими числами. Для модулів цих чисел ми маємо

 .

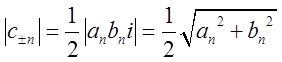Згадуючи інтерпретацію розкладання функції в тригонометричний ряд Фур'є як представлення руху у виді суми (суперпозиції) гармонійних коливань, ми бачимо, що модулі коефіцієнтів комплексного ряду Фур'є є амплітудами відповідних гармонік.

Безпосереднє розвинення функцій у комплексний ряд Фур'є на підставі формули (3.12) часто виявляється зручніше, ніж обчислення коефіцієнтів цього ряду через коефіцієнти дійсного ряду Фур'є по формулах (3.11).

П.5. Знайти розвинення в комплексний ряд Фур'є функції на сегменті . При кожнім ми тут маємо

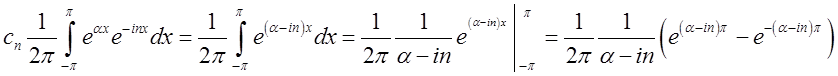
Зауважимо, що для будь-якого цілого  .

Тому       .

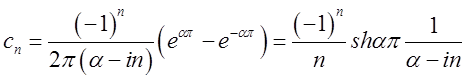Таким чином, шуканим розкладанням буде        .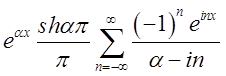

3.3. Представлення функцій інтегралом Фур'є

Представлення функції  в сегменті  рядом Фур'є (3.5)

                                                      

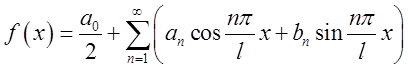
можна витлумачити в такий спосіб. Якщо функція  в сегменті є «досить гарної» (саме, якщо вона в цьому проміжку задовольняє умовам Дирихле), то для того, щоб її в цьому сегменті цілком описати, досить указати деякий, цілком визначений набір її характеристик, коефіцієнтів Фур'є (див. (3.6)):

,      ,     

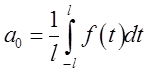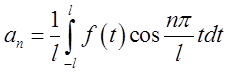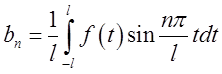
Таким чином, коефіцієнти Фур'є несуть у собі досить інформації про поводження функції у відповідному кінечному сегменті, як би великий він ні був.

Частоти гармонік ряду Фур'є (3.5) функції на сегменті довжини   складають послідовність 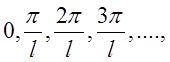      яка є арифметичною прогресією з різницею   .

Зазначимо, що при збільшенні числа , тобто при збільшенні довжини сегмента розвинення функції, різниці між частотами сусідніх гармонік зменшуються, тобто гармоніки починають йти усе більш густо.

Положення справ різко змінюється, якщо сегмент розкладання функції, необмежено розширюючи в обидва боки, охоплює всю дійсну пряму і перетворюється в нескінченний проміжок . У цьому випадку природно очікувати, що різниця між частотами сусідніх гармонік буде прямувати до нуля, тобто що послідовність гармонік з дискретної, що складається з окремих ізольованих чисел, перетвориться в неперервну множину усіх дійсних невід’ємних чисел. Природно припустити при цьому, що замість ряду Фур'є нам оведеться розглядати деякий інтеграл. Цей інтеграл, до розгляду якого ми зараз перейдемо, називається інтегралом Фур'є.

Очевидно, для того, щоб  функція могла бути представлена інтегралом Фур'є в нескінченному проміжку   ця функція повинна задовольняти деяким умовам, подібним до умов Дирихле, а крім того, і ще деяким додатковим умовам, необхідним для запобігання можливих неприємностей, що виникають у зв'язку з тим, що при необмеженому зростанні    всі інтеграли виду (3.6) виявляються вже невласними і про їхню збіжність потрібно подбати спеціально.

3.4. Найпростіші достатні умови зображення функції інтегралом Фур'є

Нехай функція , визначена на нескінченному проміжку , задовольняє наступним умовам:

1)  існує невластивий інтеграл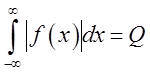 

(ця властивість функції    називається її абсолютної інтегровністю)

          2) у будь-якому кінцевому сегменті функція    розкладається в ряд Фур'є (практично досить зажадати, щоб функція в будь-якому кінцевому сегменті задовольняла умовам Дирихле).

При дотриманні цих умов ми можемо міркувати в такий спосіб.Фіксуємо деяке довільне    і напишемо розкладання функції  в ряд Фур'є в сегменті    в виді (3.5):

  ,                                                 

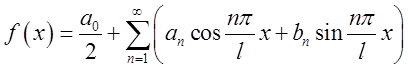де коефіцієнти визначаються по формулах (3.6). Зрозуміло, що при цьому коефіцієнти    і    залежать не тільки від функції але і від параметра (значення фігурує в межах інтегралів у формулах (3.6).Підставимо тепер у цей ряд  вираження для коефіцієнтів, що даються формулами (3.6). Ми одержимо

 

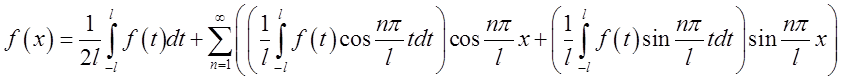
або після очевидних перетворень

                   

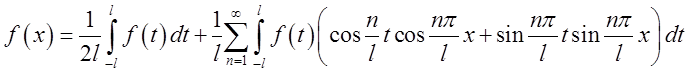
чи         .

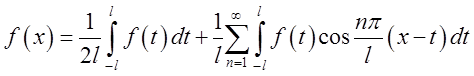Уводячи залежну від  змінну : 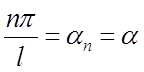,                                    (3.13)

і вважаючи, що 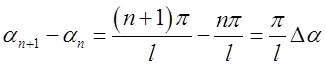    , маємо

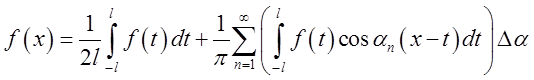 .                               (3.14)

В міру зростання інтеграл 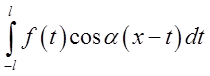       усе менше відрізняється від невластивого інтеграла .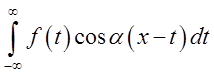

Крім того, сума, що стоїть в правій частині формули (3.14), нагадує інтегральну суму. У ній з ростом  число доданків збільшується, а кожен доданок зменшує свою «питому вагу». Тому природно припускати, що при зростанні ця сума в (3.14) прямує до інтеграла по :