Тригонометричні ряди Фур’є. Комплексна форма запису ряду Фур’є. Спектральна функція, страница 6

Обчислюючи останній інтеграл дворазовим інтегруванням частинами, ми одержуємо

 .

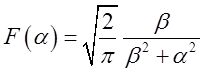Аналогічно для синус – перетворення цієї функції –

.

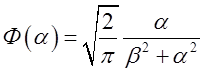 Перетворення  Фур’є широко застосовується в прикладних методах математики. На його основі створене так зване операційне числення  У даний час під операційним численням розуміється сукупність методів прикладного математичного аналізу, що дозволяють ощадливими і безпосередньо ведучими до мети засобами одержувати розв’язок лінійних диференціальних рівнянь та їх систем, а також різницевих і деяких типів інтегральних рівнянь.

           Операційне числення знайшло широке застосування в теорії автоматичного регулювання, де з його допомогою виробляється аналіз перехідних і сталих процесів в автоматичних системах.

          Сутність операційного методу полягає в наступному. Нехай задана деяка функція

f(t) дійсної перемінний t, причому така, що для неї існує перетворення Фур’є.

 Використовуючи  це перетворення, можна кожній перетворюваній по Фур’є.  функції  (у цьому випадку функція f (t) називається «оригіналом») поставити у відповідність функцію F (s) комплексної перемінний s (при цьому функція F (s) називається «зображенням» функції ). Перетворення Фур’є володіє рядом чудових властивостей. Наприклад, диференціюванню оригіналу f (t) по змінній tвідповідає операція множення зображення F(s) на комплексну змінну s, а інтегруванню оригіналу відповідає операція ділення F (s) на s. Таким чином, операції диференціювання й інтегрування оригіналу заміняються в просторі зображень оригіналу більш простими операціям алгебри – відповідно множенням і діленням зображення на s. Це дозволяє диференціальне рівняння, записане відносно шуканої функції f(t), замінити в просторі зображень на алгебраїчне рівняння щодо зображення F(s). Вирішивши це алгебраїчне рівняння і знайшовши F(s) ми одержимо зображення рішення вихідного диференціального рівняння. Для визначення самого рішення можна скористатися зворотним перетворенням Фур’є, що встановлює зв'язок між зображенням F(s) і йому відповідним оригіналом f(f):

У багатьох випадках при знаходженні зображення f (t) можна уникнути безпосереднього обчислення цього інтеграла, скориставшись таблицею відповідностей «оригінал — зображення», яка є в відповіній літературі.

Метод рішення звичайних диференціальних рівнянь за допомогою операційного числення зводиться, таким чином, до наступної  схеми: до рівняння (або системи) відносно f(x) і початкових умов застосовуємо перетворення Фур’є; одержуємо алгебраїчне рівняння (або систему) відносно зобhаження F(s) ; розвязуємо це рівняння (або систему) і знаходимо F(s); виконуємо відносно знайденого зображення F(s) обернене перетворення і знаходимо f(t).

3.11.  Спектральна функція

Покладемо 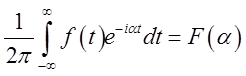       Тоді

 .

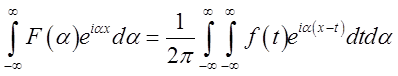У силу (3.24) останній інтеграл є . Таким чином,

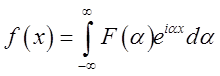 .                                                                                   (3.31) 

З механічної точки зору функція  при будь-якім значенні a описує деяке гармонійне коливання. Відповідно до цього інтегральне представлення (3.31) функції можна розуміти як представлення описуваного цією функцією руху у вигляді нескінченної неперервної системи незалежних коливань з різними частотами. Функція  показує при цьому, з якою інтенсивністю відбуваються коливання, що відповідають різним значенням a. Неважко перевірити, що модуль  є амплітуда коливання, що відповідає даному значенню a.

Функція називається спектральною функцією для вихідної функції .

Запитання для самоперевірки.

1. Що називається тригонометричним рядом Фур’є для функції для ?
2. Як обчислюються числові коефіцієнти розвинення в ряд Фур’є для ?
3. Сформулюйте достатні умови, яким повинна задовольняти  для  для того, щоб її можна було розвинути в ряд Фур’є .
4. Як зміниться вид розвинення функції і вид формул для обчислення коефіцієнтів для , якщо  ?.
5. Як обчислюються числові коефіцієнти розвинення непарної в ряд Фур’є для ?
6.  Як обчислюються числові коефіцієнти розвинення парної в ряд Фур’є для ?
7. Як розвинути в ряд Фур’є  для , або в загальному випадку ?
8. Що означає термін: розвинути в ряд Фур’є по косинусах для , або в загальному випадку ?
9. Що означає термін: розвинути в ряд Фур’є по синусах для , або в загальному випадку ?
10. Який вид має ряд Фур’є дляв комплексній формі ?