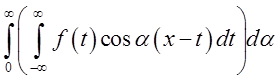Тригонометричні ряди Фур’є. Комплексна форма запису ряду Фур’є. Спектральна функція, страница 4

 .

Далі, перший доданок у (3.14) вправій частині у міру росту прямує до нуля. В цьому легко переконатися,

 .

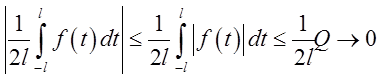Таким чином, у граничному переході, при , формула (3.14) перетворюється в наступну:

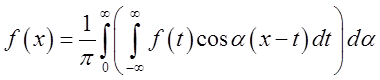                                                                   (3.15)                                                                   

Ця формула називається інтегральною формулою Фур'є, а інтеграл, що стоїть в ній - інтегралом Фур'є. Представлення функції у виді правої частини формули (3.15) звичайно називається розвиненням цієї функції в інтеграл Фур'є.

Ясно, що все тільки що сказане тут стосувалося тільки тих точок ,  у яких функція  неперервна. Для точок розриву справедлива, як і у випадку рядів Фур'є, інтегральна формула, що описує напівсуму меж функції праворуч і ліворуч:

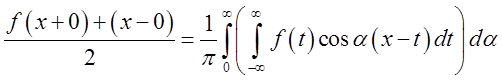                                   (3.16)                         

Отже, ми приходимо до формулювання наступної теореми.

Теорема Фур'є. Якщо функція на нескінченному проміжку  є обмеженої й інтегровна абсолютно, а в кожнім кінцевому проміжку задовольняє умовам Діріхле, то для кожного  має місце рівність (3.15), якщо є точка неперервності функції , і рівність (3.16), якщо є точка розриву цієї функції.

Зауважимо, що у формулі (3.15) внутрішній інтеграл являє собою деяку функцію від a. Тому що ця функція залежить не від самої змінної a, а від її косинуса, вона повинна бути парної. Тому ми можемо формулу (3.15) переписати в наступному виді:

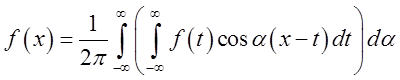                                                    (3.17)                                                  

Ми привели правдоподібні міркування на користь справедливості теореми Фур'є, що, зрозуміло, не можна вважати її доказом. Доказ теореми Фур'є досить складний і виходить за межі нашого курсу.

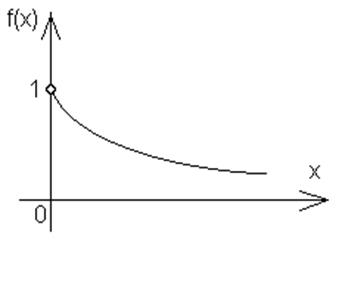П.6.  Нехай 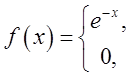якщо 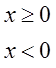  . Графік функції  зображений на рис..3.4.

Очевидно, що при будь-якому 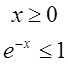  і  .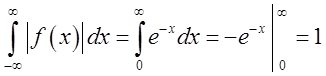

Отже, функція  в проміжку є обмежена й інтегровна абсолютно. Крім того, функція монотонно спадає, і тому функція 

            Рис. 3.4.                              тривіальним образом задовольняє умовам Дирихле.

Зі сказаного випливає, що, відповідно до теореми Фур'є, функція розвивається в інтеграл Фур'є. Випишемо це розвинення в явному виді (тобто без внутрішнього інтеграла, що знаходиться  в правій частині цієї формули). Ми маємо в розглянутому випадку

 ,

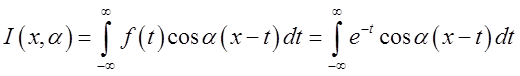чи, роблячи двічі інтегрування частинами,

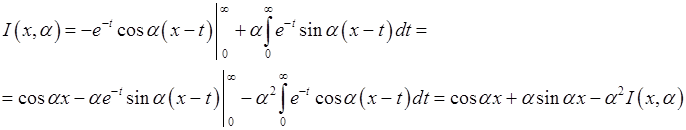
Звідси випливає, що 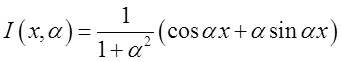. Значить, розвинення функціїв інтеграл Фур’є  в цьому випадку має вид:  .

3.5.Інтеграл Фур'є для парних функцій

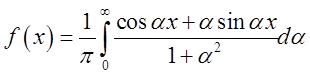Зауважимо, насамперед, що при кожнім a   , так що

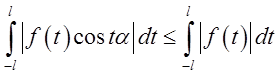 . Отже, якщо функція абсолютно інтегровна на нескінченному проміжку , то невластивий інтеграл

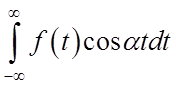                                                                             (3.18)

існує. У силу аналогічних причин існує при кожнім a і невласний інтеграл

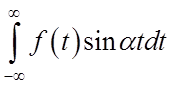                                                                              (3.19)

Згадуючи, що , перепишемо формулу (3.15) у наступному виді:

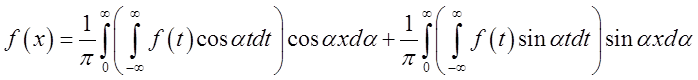      (3.20)

Припустимо тепер, що функція  парна. Тоді парними повинні бути усі функції виду   і непарними – усі функції виду . Отже, у цьому випадку всі невластиві інтеграли (3.19) дорівнюють нулеві, а для кожного з невластивих інтегралів (3.18) ми можемо написати  .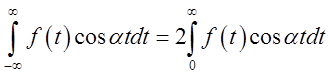

Таким чином, у випадку парної функції  формула (3.20) може бути переписана як 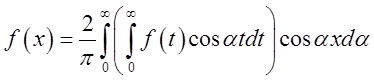                                 (3.21)

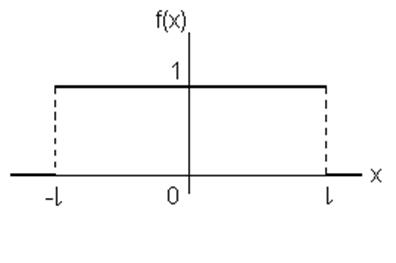П.7. Розвинути в інтеграл Фур'є парну функцію , де

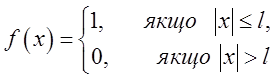 . Графік функції  див. на рис. 3.5.

Те, що функція обмежена, абсолютно інтегровна в нескінченному проміжку і задовольняє умовам Діріхле в будь-якому

                          Рис.3.5.                           кінцевому сегменті, легко перевіряється.

Отже, розвинення функції в інтеграл Фур'є існує. Для його знаходження обчислимо   .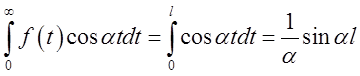

Таким чином, шуканим розвиненням є  .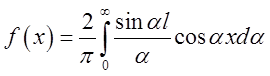

Ця формула справедлива для всіх значень   , за винятком  . У цих двох точках розриву функції  інтеграл Фур'є приймає значення, рівне .   

3.6. Інтеграл Фур'є для непарних функцій

Якщо функція непарна, то непарної ж буде і функція  і парної – функція . Тому при непарній функції в нуль обертається при будь-якім значенні a інтеграл (3.18), а для інтеграла виду (3.19) справедливо 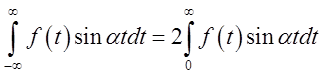 . Отже, у випадку непарної функції  формула (3.20) приймає вид:

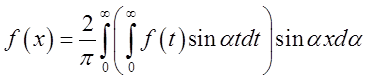                                                                 (3.22)

П.8.  Розкласти в інтеграл Фур'є непарну функцію , для якої