Тригонометричні ряди Фур’є. Комплексна форма запису ряду Фур’є. Спектральна функція, страница 2

П.2. . Розвинемо в ряд пилкоподібний імпульс заданий в інтервалі  так: .

Розв’язок. Оскільки функція парна, то всі . .

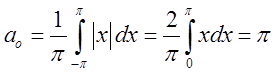                                           Рис.3.2.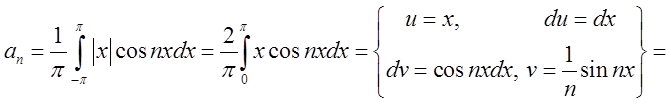    

==

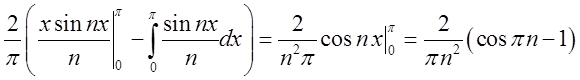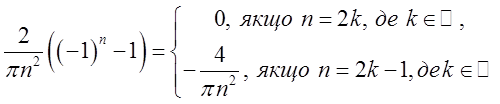= Розвинення  в ряд має вигляд

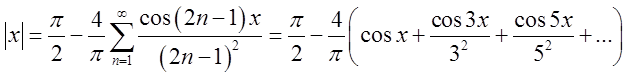
Як і в попередньому прикладі, використовуючи наглядність рис.3.2 та рис.3.3 легко простежити наближення функції  послідовними частинними сумами її ряду Фур’є. Пунктирними лініями нарисовані окремі гармоніки, а суцільними частинні суми  на рис.3.3.а  та  на рис 3.3.б. З цього розкладу при х=0 одержимо значення  через числовий ряд:

                                       Рис.3.3.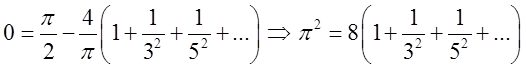                        

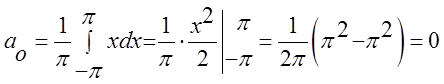
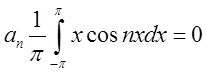
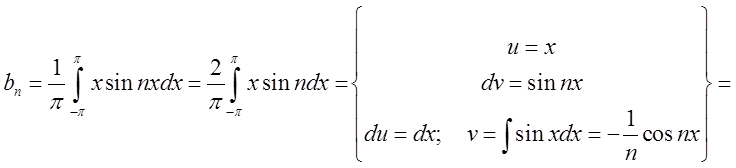
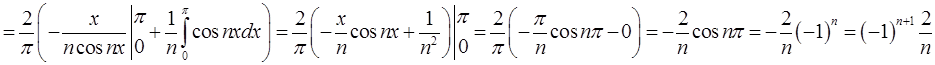
П.3. Розвинути в ряд Фурьє функцію , де

            

Підставимо в ряд і отримаємо таку відповідь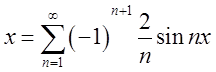   

Якщо початкова функція непарна, то розвинення в ряд буде складатися лише з одних синусів,  а якщо функція парна, то розвинення буде складатися тільки з косинусів, тобто:

якщо   - непарна, то    ; якщо - парне, то   .

Розвинення в ряд по несиметричному проміжку

            Спочатку пригадаємо той факт, що якщо функція  має період то:

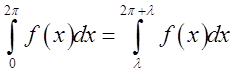. Через те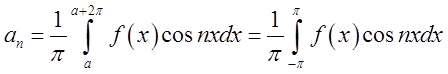  

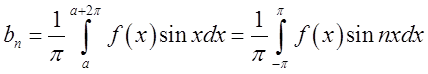      (при  )                    (3.4)

               Розвинення в ряд по довільному симетричному проміжку

Якщо задана функція  де то для неї ряд Фур’є має вид:

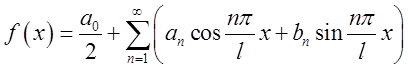                                                                          (3.5)

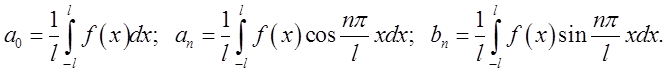                               (3.6)

П.4. Розвинемо на сегменті  функцію в ряди Фур'є по синусах і по косинусах (що буде відповідати відповідно продовженню цієї функції на сегмент по непарності і по парності).

Розвинемо цю функції по синусах. Це значить, що ми продовжили на сегмент  по непарності, крім того ми її розглядаємо як періодичну.

Розвинення для цієї функції було одержано вище   і в розгорнутому виді

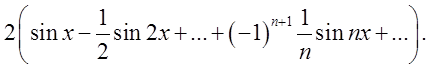                          (3.7)

Розвинемо цю функцію в ряд по косинусах. Це значить, що ми  продовжили на сегмент  по парності і знову ж таки ми її розглядаємо, як періодичну.Аналітичний запис такої функції 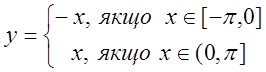. Графік її зображено на рисунку 3. 2.

Для того щоб знайти розвинення в ряд по косинусах, обчислимо інтеграли, враховуючи властивість визначеного інтеграла, якщо підінтегральна функція парна , а сегмент інтегрування симетричний 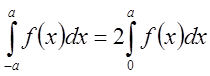, а для непарної .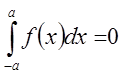

Тому, що  на сегменті  непарна маємо .

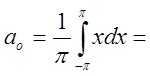
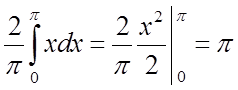. Обчислюючи 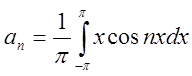, одержуємо

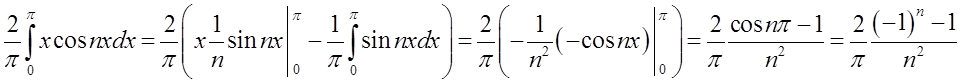 Очевидно, що останній вираз дорівнюватиме 0 коли показник степеня  п для основи (-1) буде парним і 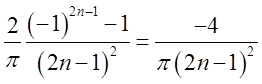 коли цей показник буде непарний.

Розвинення по косинусах буде мати вид

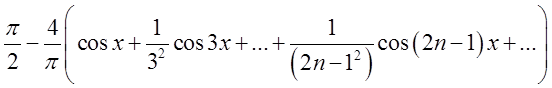 .            (3.8)

Звідси випливає один цікавий наслідок.

Позначимо суму останнього ряду через  . Після продовження функції на  по парності точка 0 буде точкою неперервності продовженої функції. Тому відповідно до теореми Діріхле  , тобто

 .                                                                       (*)

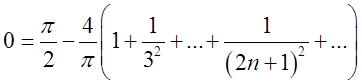Якщо позначити через 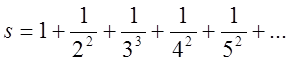 суму ряду <обернених квадратів>, то сума ряду чисел, обернених парним квадратам, буде дорівнює , переконаємось в цьому, зробивши перегрупіровку ряду і винісши із обернених парних квадратів спільний множник   +=.

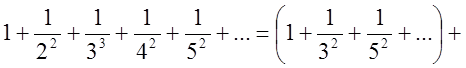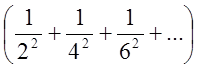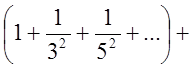
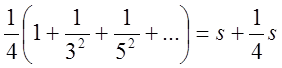 так що сума ряду, що знаходиться в дужках виразу (*), дорівнює  .  Таким чином, 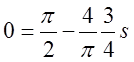  , відкіля 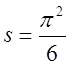 це і є сума ряду <обернених квадратів>

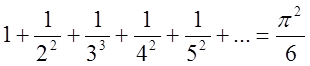                                                                                  (3.8)

3.2. Комплексна форма запису ряду Фур'є

Формули Эйлера дозволяють виражати тригонометричні функції через показникові функції з комплексним показником. Отже, у такій комплексній формі можуть бути представлені тригонометричні ряди і, зокрема, ряди Фур'є тих чи інших функцій.

 Нехай 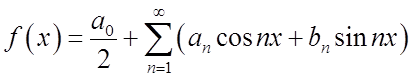                                                  (3.9)

– деякий тригонометричний ряд. Ми маємо формули Эйлера (див. 2.35-36)

      .

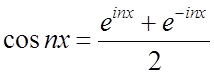
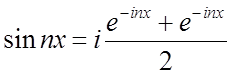 Тоді 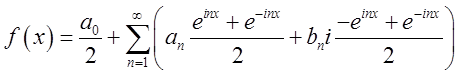  , або поєднуючи степені з однаковими показниками, 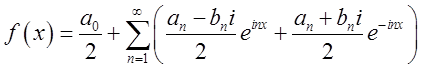 .                                  (3.10)                                   

Введемо  позначення:

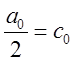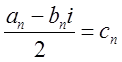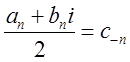 ,     ,    .                                                      (3.11)

Тоді (3.10) перетворюється в     =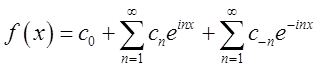

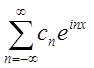
Таким чином, ми одержали розвинення функції  у функціональний ряд з комплексними членами. Він називається  рядом Фур'є в комплексній формі. Коефіцієнти цього ряду можна обчислювати не тільки по формулах (3.11) з коефіцієнтів ряду Фур'є (3.9), але і безпосередньо, минаючи знаходження  і .

Використовуючи (3.2) ми маємо

 

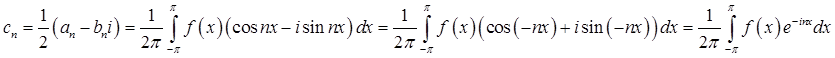
і аналогічно

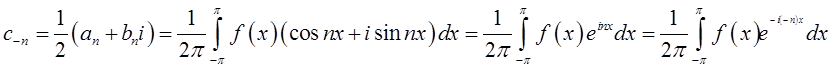
 Отже, при будь-якому цілому  , , ,…