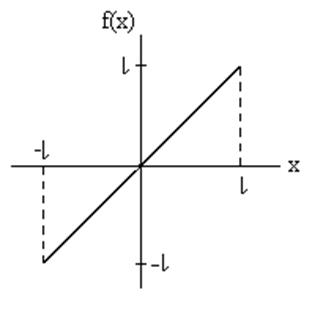
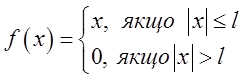 (графік цієї функції зображений на
рис.3.6.).
(графік цієї функції зображений на
рис.3.6.).
Ясно, що функція ![]() обмежена, абсолютно інтегровна і
задовольняє умовам Діріхле там, де це потрібно. Переходимо до обчислення
внутрішнього інтеграла у формулі (3.22). Ми маємо
обмежена, абсолютно інтегровна і
задовольняє умовам Діріхле там, де це потрібно. Переходимо до обчислення
внутрішнього інтеграла у формулі (3.22). Ми маємо
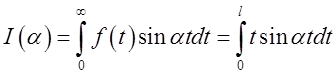 чи, інтегруючи частинами,
чи, інтегруючи частинами,
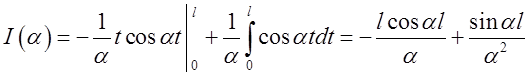 . Тому
. Тому 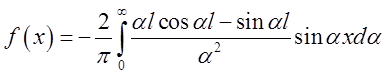 . Ця
формула
. Ця
формула
Рис. 3.6. справедлива для всіх значень ![]() ,
за винятком
,
за винятком ![]() . Для
. Для ![]() значення
правої частини формули буде вдвічі менше значення її лівої частини.
значення
правої частини формули буде вдвічі менше значення її лівої частини.
3.7. Комплексна форма інтеграла Фур'є
Повернемося до інтегральної формули Фур'є
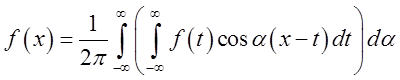 (3.23)
(3.23)
і застосуємо до наявного в цій формулі косинусу формулу Эйлера:
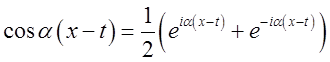 . Ми одержимо
. Ми одержимо
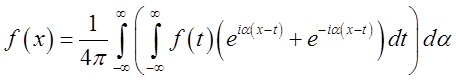 , чи
, чи 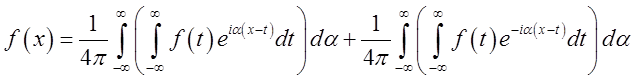 .
.
Тут, як неважко
переконатися підстановкою ![]() , інтеграли, що стоять у
правій частині, рівні один одному. Тому
, інтеграли, що стоять у
правій частині, рівні один одному. Тому
 (3.24)
(3.24)
Отримана формула
називається розкладанням функції ![]() в
інтеграл Фур'є в комплексній формі.
в
інтеграл Фур'є в комплексній формі.
П.9. Знайдемо інтеграл Фур'є в комплексній формі для функції
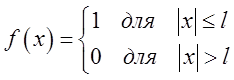
У цьому випадку обчислення внутрішнього інтеграла в правій частині формули (3.24) дає нам
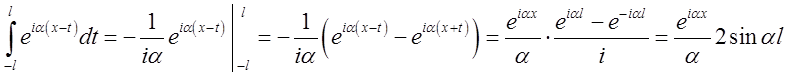 .
.
Тому формула (3.24)
набуває в даному випадку такого виду: 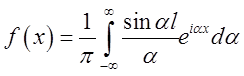 .
.
П.10.Розвинемо в інтеграл Фур'є в комплексній формі функцію 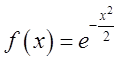 ( рис.3.7.). Ми маємо
( рис.3.7.). Ми маємо
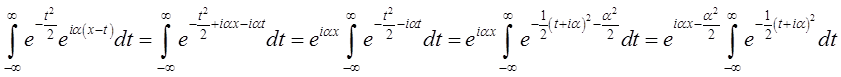 Останній інтеграл є функцією від a. Позначимо його через
Останній інтеграл є функцією від a. Позначимо його через
![]() і обчислимо його. Ми маємо
і обчислимо його. Ми маємо
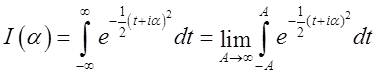 ,
,
роблячи
підстановку ![]() , ми одержимо
, ми одержимо 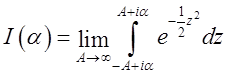 .
.
Продиференцюємо ця тотожність по a. Через те, що збіжність до границі по a є рівномірною в
Рис.3.7. будь-якому кінцевому проміжку,
диференціювання під знаком границі законно. Ми маємо 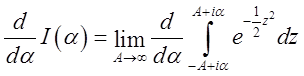 .
Виконуючи диференціювання інтеграла по верхній і нижній границях, ми одержуємо
.
Виконуючи диференціювання інтеграла по верхній і нижній границях, ми одержуємо
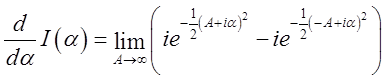 , а згадуючи формулу (3.23) і переходячи
до границі, будемо мати
, а згадуючи формулу (3.23) і переходячи
до границі, будемо мати 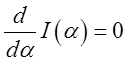 . Отже, первісна
функція повинна бути постійної:
. Отже, первісна
функція повинна бути постійної: ![]() . Зокрема, повинне бути
. Зокрема, повинне бути
![]() . Обчислимо інтеграл
. Обчислимо інтеграл ![]() . Запишемо його для цього двічі:
. Запишемо його для цього двічі:
 , і перемножимо почленно ці рівності. Ми
одержимо
, і перемножимо почленно ці рівності. Ми
одержимо 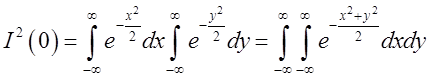 .
.
Переходячи в подвійному інтегралі до полярних координат, ми маємо
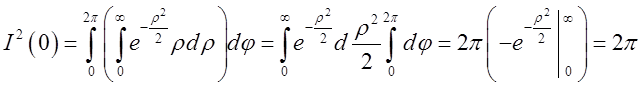 , відкіля
, відкіля![]() .
Таким чином,
.
Таким чином,
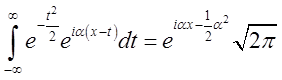 (3.25)
(3.25)
і шуканим розвиненням
в інтеграл Фур'є є 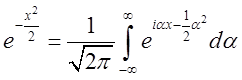 .
.
3.8.Поняття про перетворення Фур'є
Перепишемо формулу
(3.24), заміняючи a на ![]() , у наступному виді:
, у наступному виді:
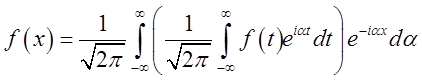 , і покладемо
, і покладемо
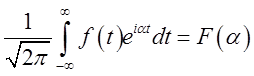 (3.26)
(3.26)
Тоді, очвидно,
буде 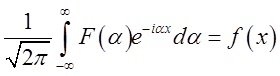 (3.27)
(3.27)
Визначення. Перехід від функції ![]() до функції
до функції ![]() , описуваний формулою (3.26), називається перетворенням
Фур'є функції
, описуваний формулою (3.26), називається перетворенням
Фур'є функції ![]() . Часто перетворенням Фур'є
функції
. Часто перетворенням Фур'є
функції ![]() називається сама функція
називається сама функція ![]() . Зворотний перехід від функції
. Зворотний перехід від функції ![]() до функції
до функції ![]() ,
описується формулою (3.27), називається зворотним перетворенням Фур'є. Також
зворотним перетворенням Фур'є функції
,
описується формулою (3.27), називається зворотним перетворенням Фур'є. Також
зворотним перетворенням Фур'є функції ![]() називається
функція
називається
функція ![]() .
.
П.11. Узагалі говорячи, самі функції мають мало загального з функціями, що є
їх перетвореннями Фур'є. Однієї з деяких функцій, що збігаються зі своїми
перетвореннями Фур'є, є 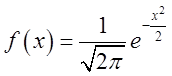
У тім, що для цієї функції
дійсно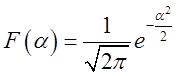 , нас переконує другий приклад з
попереднього параграфа. Справді, у цьому випадку ми маємо
, нас переконує другий приклад з
попереднього параграфа. Справді, у цьому випадку ми маємо 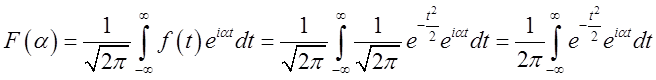 ,
,
чи, користаючись
формулою (3.25), поклавши в ній ![]() і заміняючи a на
і заміняючи a на ![]() , одержуємо необхідне.
, одержуємо необхідне.
3.9. Косинус – перетворення Фур'є
Нехай![]() - парна функція. Згадаємо формулу (3.21)
- парна функція. Згадаємо формулу (3.21)
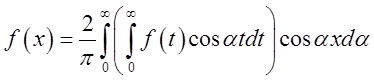 , перепишемо її у виді
, перепишемо її у виді
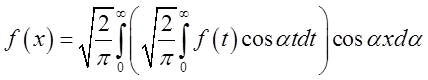 (3.28)
(3.28)
і покладемо 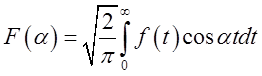 .
(3.29)
.
(3.29)
Тоді (3.28) дасть
нам 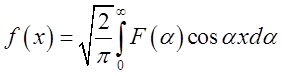 (3.30)
(3.30)
Формула (3.29) визначає косинус – перетворення Фур'є парної функції
![]() , що приводить до функції
, що приводить до функції ![]() , також названої косинус – перетворенням
функції
, також названої косинус – перетворенням
функції ![]() . Формула (3.30) визначає зворотне косинус
– перетворення.
. Формула (3.30) визначає зворотне косинус
– перетворення.
3.10.Синус – перетворення Фур'є
Для непарної
функції ![]() ми можемо послатися на формулу (3.22)
ми можемо послатися на формулу (3.22)
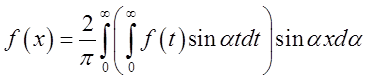 і за аналогією з попереднім визначити синус
– перетворення Фур'є
і за аналогією з попереднім визначити синус
– перетворення Фур'є 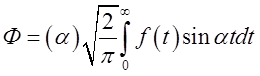
і зворотне синус –
перетворення 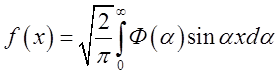 .
.
П.12. Розглянемо функцію ![]() ,
,
визначену тільки
для![]() . Останнє означає, що ми можемо,
продовжуючи нашу функцію
. Останнє означає, що ми можемо,
продовжуючи нашу функцію ![]() на область негативних
значень по чи парності по не парності, знайти як косинус – перетворення цієї
функції, так і її синус – перетворення.
на область негативних
значень по чи парності по не парності, знайти як косинус – перетворення цієї
функції, так і її синус – перетворення.
Для косинус – перетворення ми маємо
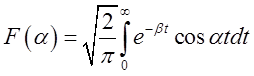 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.