Лекція 2
ФУНКЦІОНАЛЬНІ РЯДИ
План:
2.1. Збіжність функціональних рядів.
2.2. Властивості рівномірно збіжніх рядів.
2.3. Степеневі ряди.
2.4. Ряди Тейлора і Маклорена.
2.5. Стандартні розвинення елементарних функцій в степеневі ряди.
2.6. Формули Єйлера.
2.7. Застосування степеневих рядів.
2.8. Запитання для самоперевірки.
Українсько-російський словник вжитих в лекції слів, які в мовах мають різне звучання.
Певна – определённаяВідхилення – отклонение Згідно – согласно Залишок – остаток |
Зручніший – удобнееВизначити – определить Похідні – производные околі – окрестности |
Розвинення – разложениеУраховуючи – учитывая Зберігаючи – сохраняя |
Математичні факти з попередніх розділів, які використовуються в даній лекції.
1.Розв’язування нерівностей, у яких змінна величина знаходиться під знаком модуля
а) ![]()
![]() це і буде відповіддю. Можна цю
нерівність зводити до системи нерівностей:
це і буде відповіддю. Можна цю
нерівність зводити до системи нерівностей:
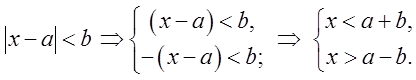
б) розвязування нерівності ![]() відрізняється
від попередннього тим, що ця нерівність зводиться не до системи, а до
сукупності нерівностей. Буде безглуздо написати по аналогії з а):
відрізняється
від попередннього тим, що ця нерівність зводиться не до системи, а до
сукупності нерівностей. Буде безглуздо написати по аналогії з а): ![]() або
або 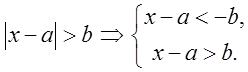 таке
перетворення нерівності є не вірним, тобто знак
таке
перетворення нерівності є не вірним, тобто знак ![]() там
стояти не повинен. Перетин множин розв’язків кожної з нерівностей, які стоять в
системі, завжди є порожня множина. Розв’язувати таку нерівність треба так:
там
стояти не повинен. Перетин множин розв’язків кожної з нерівностей, які стоять в
системі, завжди є порожня множина. Розв’язувати таку нерівність треба так: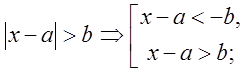
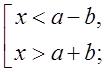
![]() .
.
2.1. Збіжність функціональних рядів
О. Функціональним називається ряд
![]()
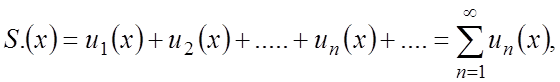
![]() (2.13)
(2.13)
де всі функції ![]() визначені на певній
множині, наприклад X.
визначені на певній
множині, наприклад X.
![]()
Нехай в (2.13) x=x0 ![]()
![]()
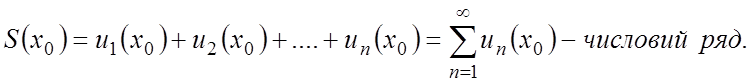
О. Функціональний ряд (2.13) називається збіжним при х=х0, якщо відповідний числовий ряд, утворений з ряду (2.13) при х=х0, є збіжним.
О. Функціональний![]() ряд
(2.13) називається збіжним на множині Х, якщо він збіжний
ряд
(2.13) називається збіжним на множині Х, якщо він збіжний ![]()
Введемо два поняття.
О. Рівномірним (чебишовським) відхиленням
функцій ![]()
![]() (2.14)
(2.14)
і середнім відхиленням – величина
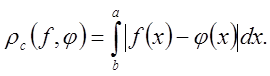 (2.15)
(2.15)
Рівномірне відхилення можна застосувати до обмежених функцій, в разі ж збіжності відповідного інтеграла і у випадку необмежених функцій –середнє. Замінивши в (2.15) підінтегральну функцію на її максимальне значення і оцінивши інтеграл, дістаємо
![]()
![]() (2.16)
(2.16)
звідки випливає, що при малих ![]() обернене твердження не завжди
правильне,тобто рівномірне відхилення є жорсткішою оцінкою, ніж
середнє.
обернене твердження не завжди
правильне,тобто рівномірне відхилення є жорсткішою оцінкою, ніж
середнє.
О. Функціональний ряд (2.13) називається
рівномірно збіжним на ![]() якщо
якщо
![]()
і збіжним в середньому, якщо
![]()
З нерівності (2.16) випливає, що рівномірно збіжний ряд є збіжним і в середньому, обернене твердження не завжди правильне.
Наступна теорема виражає достатню умову рівномірної збіжності ряду (2.13).
Т. (Вейерштрасса). Якщо ![]() х
х![]() всі члени ряду (2.13) задовольняють
нерівність
всі члени ряду (2.13) задовольняють
нерівність ![]() причому ряд
причому ряд ![]() збіжний,
то ряд (2.13) рівномірно збіжний на
збіжний,
то ряд (2.13) рівномірно збіжний на![]()
Дов-ня. За достатньою ознакою збіжності ряду,
згідно з умовами теореми, ряд (2.13) абсолютно збігається до ![]()
Доведемо, що ця збіжність є рівномірною. Розглянемо рівномірне відхилення
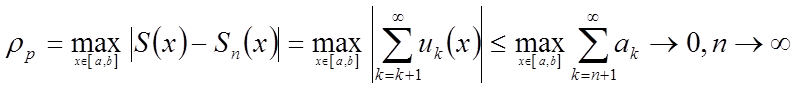
Як залишок збіжного числового ряду.![]()
П.1. Дослідити на рівномірну збіжність 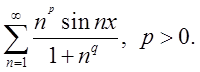
Розв’язання. Маємо
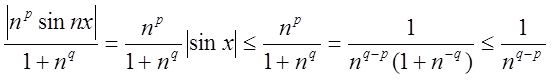 так, як числовий ряд
так, як числовий ряд 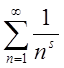 збігається при s>1,
то при
збігається при s>1,
то при ![]() ряд рівномірно збіжний на
ряд рівномірно збіжний на ![]()
2.2. Властивості рівномірно збіжних рядів.
Т. 1. (неперервність суми). Сума рівномірно збіжного
на ![]() ряду, складеного з неперервних на
ряду, складеного з неперервних на ![]() функцій, є неперервною на
функцій, є неперервною на ![]() .
.
§
Маємо ![]()
В останньому співвідношенні перейдемо до границі при ![]()
Оскільки скінченна сума неперервних функцій неперервна, то ![]() при
при ![]()
З рівномірності збіжності ряду маємо ![]() .
.
Отже ![]() . Тепер в рівності
. Тепер в рівності ![]() перейдемо до границі при
перейдемо до границі при![]()
![]() Оскільки ліва частина
від п не залежить, то
Оскільки ліва частина
від п не залежить, то ![]()
Т. 2.(про граничний перехід). Рівномірно збіжний на ![]() ряд допускає на цьому інтервалі граничний
перехід для
ряд допускає на цьому інтервалі граничний
перехід для ![]() , тобто
, тобто ![]() .
.
Т. 3.(про диференціювання ряду). Збіжний на ![]() ряд допускає на цьому інтервалі по членне
диференціювання за умови, що одержаний ряд буде рівномірно збіжний на
ряд допускає на цьому інтервалі по членне
диференціювання за умови, що одержаний ряд буде рівномірно збіжний на ![]() , тобто
, тобто ![]() .
.
В теоремі суттєвим є те, що одержаний після диференціювання ряд повинен бути рівномірно збіжним. Переконаємось в цьому на прикладі.
П.2. Продиференцюємо ряд 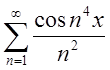 ,
одержимо
,
одержимо 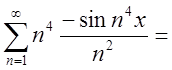
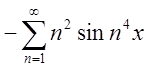 .Початковий ряд збіжний
так, як
.Початковий ряд збіжний
так, як 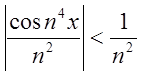 , а продиференційований взагалі
розбігається.
, а продиференційований взагалі
розбігається.
Т. 4.(про інтегрування ряду). Рівномірно збіжний на ![]() ряд інтегрованих функцій можна
зінтегрувати на цьому інтервалі тобто для
ряд інтегрованих функцій можна
зінтегрувати на цьому інтервалі тобто для ![]() маємо
маємо 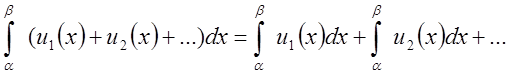 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.