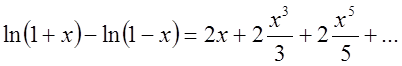
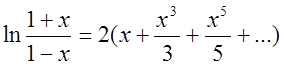 . Обчислимо при якому
значенні х вираз під логарифмом дорівнює 3.
. Обчислимо при якому
значенні х вираз під логарифмом дорівнює 3. 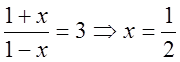 .
Підставивши це значення в робочу формулу одержимо
.
Підставивши це значення в робочу формулу одержимо 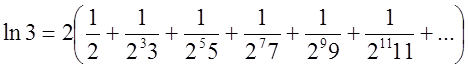 =
=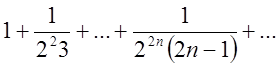
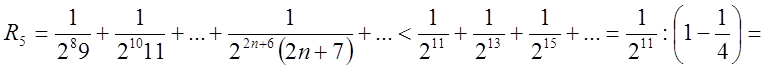
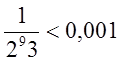 . А
тому
. А
тому 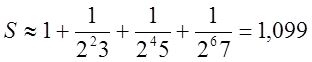 .
.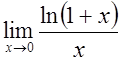 .
.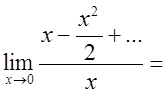
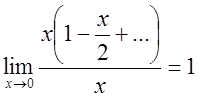 .
. 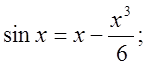
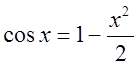 ;
; 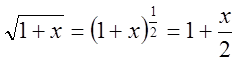 ;
; 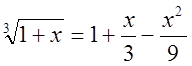 .
.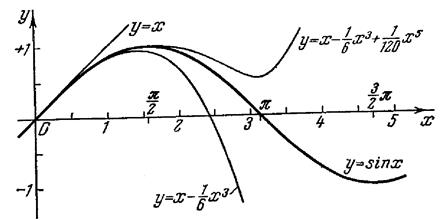
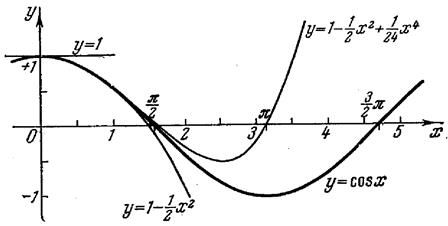
Рис.1.2 Рис.1.3.
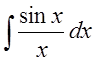 .
.Розв’язання. Цей інтеграл не виражається через елементарні функції.
В неелементарних же маємо
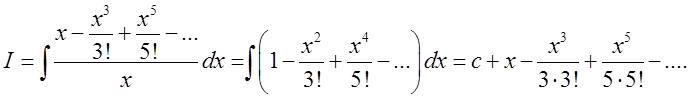
П.11. Знайти частинний розв’зок рівняння ![]()
Роз-ня. Це лінійне рівняння. Розв’язок будемо шукати у вигляді ряду
![]() (*)
(*)
похідна від якого буде ![]()
Підставивши початкові умови в ![]() дістаємо
дістаємо
![]() Підставимо тепер
Підставимо тепер ![]() і
і
![]() в рівняння. Маємо
в рівняння. Маємо
![]()
Порівняємо коефіцієнти при однакових степенях ![]() в обох частинах останньої рівності
в обох частинах останньої рівності
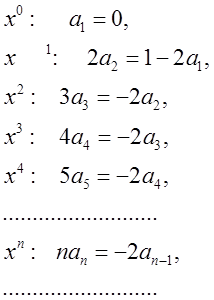
Знайдемо відповідні коефіцієнти: 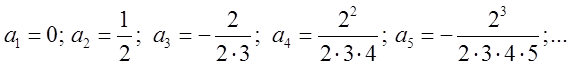
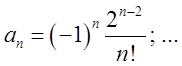 Тепер підставимо їх в рівність (*).
Використовуючи (2.22), остаточно матимемо
Тепер підставимо їх в рівність (*).
Використовуючи (2.22), остаточно матимемо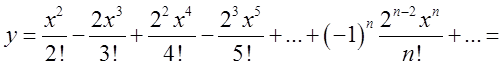 {винесемо
за дужку
{винесемо
за дужку ![]() , в дужках додамо та віднімемо до виразу
доданки
, в дужках додамо та віднімемо до виразу
доданки ![]() , підганяючи суму під
, підганяючи суму під ![]() }=
}=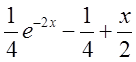
П.12. Знайти розв’язок рівняння![]() , розвязок представити у вигляді
многочлена другого степеня.
, розвязок представити у вигляді
многочлена другого степеня.
Розв. Шукану
функцію представимо через ряд 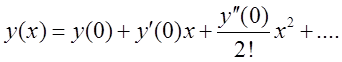
Так, як ![]() за умовою, то з умови
за умовою, то з умови ![]() ;
; ![]()
Остаточно ![]() Відп.
Відп.![]()
Запитання для самоперевірки.
Розвяжіть самостійно.
1.Знайти інтервал збіжності степеневого ряду і дослідити його збіжність на кінцях інтервалу.
1.1. 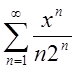 ; Вілп.
; Вілп. ![]() .1.2.
.1.2. 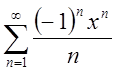 ;Відп.
;Відп.![]() 1.3.
1.3. 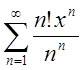 ; Відп.
; Відп.![]() .
.
2. Розвинути в ряд за степенями х вказані функції та знайти область їх збіжності.
2.1. 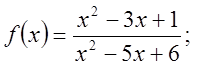 Відп.
Відп. 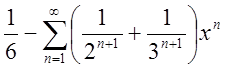 ,
, ![]() .
.
2.2. ![]() Відп.
Відп. 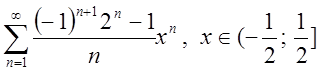 .
.
3. Обчислити з точністю до 0,001, застосовуючи ряди.
3.1.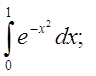 Відп. 0,7468. 3.2.
Відп. 0,7468. 3.2. ![]() Відп. 2,087.
Відп. 2,087. ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.