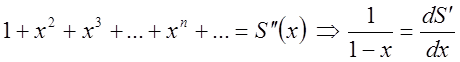 . Це диференційне рівняння з
відокремлюючими змінними, яке легко інтегрується. При інтегруванні два рази,
з’явиться дві довільні сталі, значення яких можна знайти лише маючи початкові
умови. Такі умови легко створити самому, підставивши яке-небудь значення
(наприклад х=0) в (*) і в (**).
. Це диференційне рівняння з
відокремлюючими змінними, яке легко інтегрується. При інтегруванні два рази,
з’явиться дві довільні сталі, значення яких можна знайти лише маючи початкові
умови. Такі умови легко створити самому, підставивши яке-небудь значення
(наприклад х=0) в (*) і в (**).
Ми одержимо ![]() . Розв’язуємо рівняння.
. Розв’язуємо рівняння.
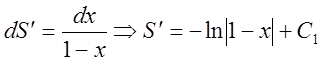 . Обчислюємо С1
. Обчислюємо С1 ![]()
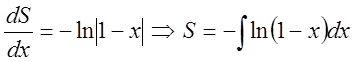 . Інтеграл обчислюємо частинами
. Інтеграл обчислюємо частинами![]() Обчислюємо
Обчислюємо ![]() .
. ![]() . Таким чином
. Таким чином ![]() .
.
Сума ряду даного за умовою буде ![]() . Це і
є відповідь.
. Це і
є відповідь.
Зауваження. Початковий ряд при х=1 збігається однак знайдена сума при х=1 невизначена. Це повязано з тим, що поблизу кінців інтервалу збіжності – ряд збігається нерівномірно. А при диференціюванні нерівномірно збіжного ряду в деяких точках (як правило на кінцях інтервалу) втрачається його збіжність.
П.5. Знайти суму ряду 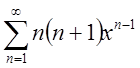
Розв. Область збіжності цього ряду ![]() .
Цей ряд збігається рівномірно скрізь в області збіжності крім точок, які лежать
поблизу кікців інтервалу збіжності. Придивимось до ряду
.
Цей ряд збігається рівномірно скрізь в області збіжності крім точок, які лежать
поблизу кікців інтервалу збіжності. Придивимось до ряду ![]() ,
якщо ми його проінтегруємо, по одному множнику у кожному доданку скоротиться і
одержимо простіший ряд. Нехай
,
якщо ми його проінтегруємо, по одному множнику у кожному доданку скоротиться і
одержимо простіший ряд. Нехай ![]() тоді
тоді ![]() . Виконавши інтегрування, одержимо
. Виконавши інтегрування, одержимо
![]() . Очевидно, що ще одне
інтегрування ліву частину останьої рівності перетворить в звичайну нескінченно
спадну геометричну прогресію, суму якої знайти дуже легко.
. Очевидно, що ще одне
інтегрування ліву частину останьої рівності перетворить в звичайну нескінченно
спадну геометричну прогресію, суму якої знайти дуже легко. ![]()
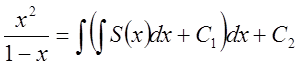 . Це найпростіше інтегральне
рівняння (невідома функція знаходиться під знаком інтеграла). Розвязується воно
застосуванням до обох частин операції оберненої до інтегрування –
диференціювання.
. Це найпростіше інтегральне
рівняння (невідома функція знаходиться під знаком інтеграла). Розвязується воно
застосуванням до обох частин операції оберненої до інтегрування –
диференціювання. 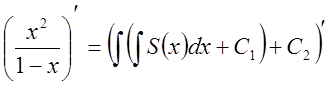 . Виконаємо операцію
диференціювання
. Виконаємо операцію
диференціювання 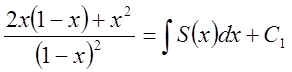 . Або після спрощення
. Або після спрощення 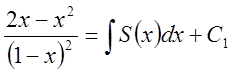 . Застосовуючи повторно диференціювання,
одержимо
. Застосовуючи повторно диференціювання,
одержимо 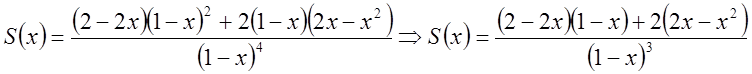
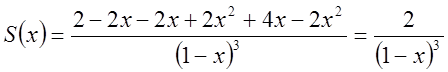 . Це і є відповідь.
. Це і є відповідь.
П.6. Використовуючи стандартні розвинення в ряди, розкласти за степенями х функцію
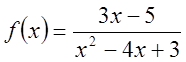 .
.
Розв. Представимо функцію ![]() у
вигляді суми двох функцій. Таке представлення можливе бо знаменник дробу можна
записати у вигляді добутку двох двочленів
у
вигляді суми двох функцій. Таке представлення можливе бо знаменник дробу можна
записати у вигляді добутку двох двочленів
![]() і потім, застосувавши метод
невизначених коефіцієнтів прийдемо до суми.
і потім, застосувавши метод
невизначених коефіцієнтів прийдемо до суми. 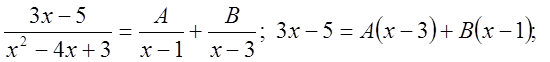 перегрупуємо
перегрупуємо
![]() . Для знаходження невизначених
коефіцієнтів А і В одержуємо систему
. Для знаходження невизначених
коефіцієнтів А і В одержуємо систему 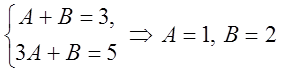 . Таким чином
. Таким чином 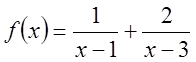 . Перетворимо ці доданки так, щоб можна
було застосувати до кожного з них формулу суми нескінченно спадної геометричної
прогресії.
. Перетворимо ці доданки так, щоб можна
було застосувати до кожного з них формулу суми нескінченно спадної геометричної
прогресії. 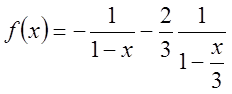 =
=![]()
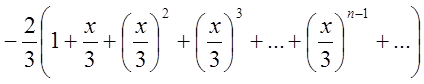 ={область збіжності першого ряду
={область збіжності першого ряду ![]() , другого
, другого ![]() .
Зрозуміло, що область збіжності суми буде
.
Зрозуміло, що область збіжності суми буде ![]() }=
}=
=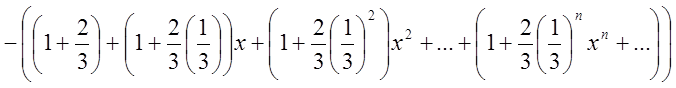 =
=
=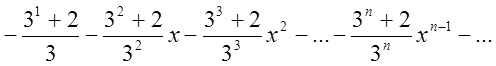 Це і є відповідь.
Це і є відповідь.
![]()
2.6. Формули Ейлера
Додамо дві рівності 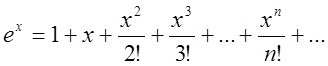 та
та
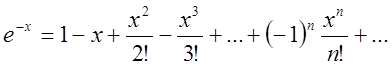 .
.
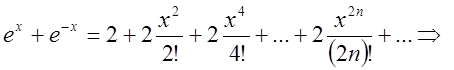
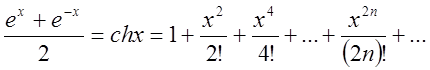 (2.31)
(2.31)
Якщо ж ми ці дві рівності віднімемо, то одержимо розвинення
в степеневий ряд ![]() .
.
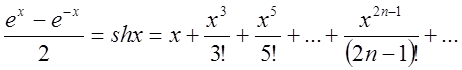 (2.32)
(2.32)
Для подальшого розуміння матеріалу пригадаємо деякі елементи
теорії функцій комплексної змінної, а саме: ![]() далі
дуже легко знайти яку завгодно степінь уявної одиниці – треба її показник
розділити на 4 і якщо в остачі буде 0, то величина степеня буде дорівнювати 1;
якщо остача 1, то величина степеня буде і; якщо два, то буде –1; якщо три, то
буде –і. Розпишемо ряди
далі
дуже легко знайти яку завгодно степінь уявної одиниці – треба її показник
розділити на 4 і якщо в остачі буде 0, то величина степеня буде дорівнювати 1;
якщо остача 1, то величина степеня буде і; якщо два, то буде –1; якщо три, то
буде –і. Розпишемо ряди ![]() при
при ![]() .
.
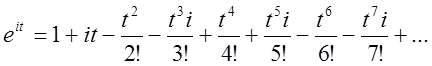
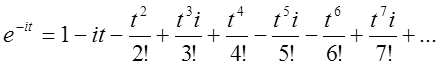
Зробимо в обох виразах очевидні перегрупування і винесемо за дужки і.
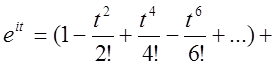
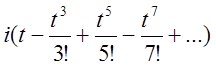
![]() (2.33)
(2.33) 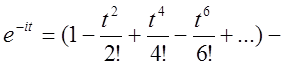
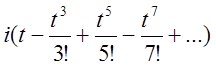
![]() (2.34)
(2.34)
Додавши (2.33) до (2.34) одержимо 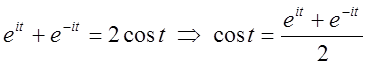 (2.35)
(2.35)
Віднявши (2.34) від (2.33) одержимо 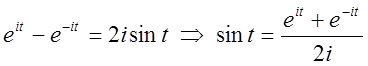 (2.36)
(2.36)
Одержані формули (2.33)–(2.36) називаються формулами Ейлера. Вони виражають тригонометричні функції через показникові і навпаки.
Цікавий зв’язок мають гіперболічні функції з
тригонометричними. Він проявиться, якщо ми в (2.31) та в (2.32) зробимо заміну ![]() .
.
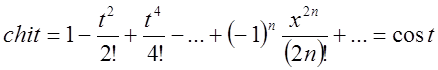 , тобто
, тобто ![]() (2.37)
(2.37)
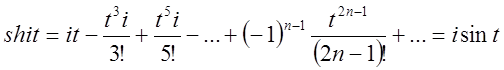 , тобто
, тобто Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.