![]()
У загальному випадку ![]() !
!![]()
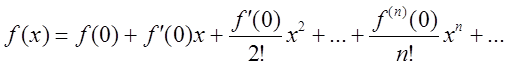 (2.20)
(2.20)
Ряд (2.20) називається рядом Маклорена для ![]() Якщо
Якщо ![]() або
деякі її похідні не визначени при
або
деякі її похідні не визначени при ![]() то на основі ряду
(2.18) знаходимо
то на основі ряду
(2.18) знаходимо
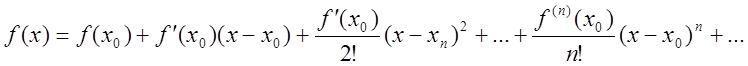 (2.21)
(2.21)
Ряд (2.21) називається рядом Тейлора для ![]() .
.
Справедлива така теорема.
Т. Ряд Тейлора (Маклорена) для ![]() збігається саме до
збігається саме до ![]() ,
якщо існує
,
якщо існує ![]() таке, що
таке, що
![]()
у деякому околі точки ![]()
Зображення функції ![]() у
вигляді (2.20) чи (2.21) називається розвиненням
у
вигляді (2.20) чи (2.21) називається розвиненням ![]() у
відповідний ряд (за відповідними стпенями).
у
відповідний ряд (за відповідними стпенями).
2.5. Стандартні розвинення елементарних функцій в степеневі ряди
Виконаємо розвинення деяких елементарних функцій у ряди Маклорена.
1. Нехай ![]() . Маємо
. Маємо![]() ,
, ![]() ,
, ![]() ,…,
,…,![]() ,…, а тому
,…, а тому
![]()
![]()
![]() …=
…=![]()
Згідно з (2.20) ![]() =
=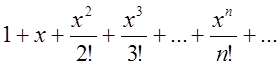 (2,
22)
(2,
22)
Знайдемо інтервал збіжності цього ряду. За ознакою Даламбера
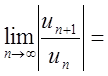
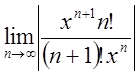 =
=
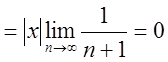 . Яке б не було х остання
рівність завжди виконується, а тому
. Яке б не було х остання
рівність завжди виконується, а тому ![]() .
.
2.
Нехай ![]() . Тоді
. Тоді ![]() ,
,
![]() ,
, ![]() ,
,![]() , …,
, …,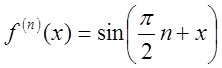 ,… При
х = 0 дістанемо
,… При
х = 0 дістанемо ![]()
![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() …
Підставивши в (2.20) одержимо
…
Підставивши в (2.20) одержимо ![]() =
=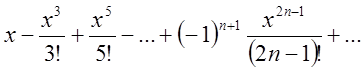 (2.23)
(2.23)
3.
Нехай ![]() . Тоді
. Тоді ![]() ,
,
![]() ,
, ![]() ,
,![]() , …,
, …,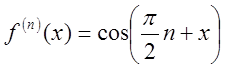 ,… При
х = 0 дістанемо
,… При
х = 0 дістанемо ![]()
![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() …
Підставивши в (2.20) одержимо
…
Підставивши в (2.20) одержимо ![]() =
=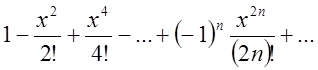 (2.24)
(2.24)
4. Нехай
маємо ![]() . Послідовно знайдемо похідні
. Послідовно знайдемо похідні
![]()
![]()
![]()
![]()
![]()
![]()
…………………………………. …………………………
![]()
![]()
………………………………………………. …………………………………….
Ураховуючи, що ![]() , після підстановки
знайдених коефіцієнтів в (2.20) одержимо
, після підстановки
знайдених коефіцієнтів в (2.20) одержимо 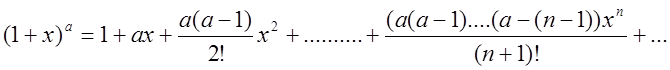 (2.25)
(2.25)
Ряд (2.25) називається біномінальним. Дослідимо його на збіжність. Знаходимо
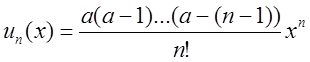 ,
, 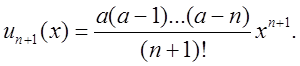 Отже
Отже
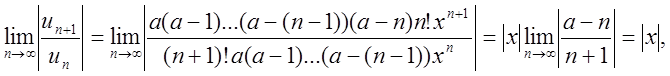 звідки
звідки![]()
З ряду (2.25) при різних значеннях ![]() ,
застосовуючи диференціювання та інтегрування, можна одержати розвинення
багатьох функцій в ряд не застосовуючи, як це було вище, громіздкого обчислення
коефіцієнтів. Наприклад при
,
застосовуючи диференціювання та інтегрування, можна одержати розвинення
багатьох функцій в ряд не застосовуючи, як це було вище, громіздкого обчислення
коефіцієнтів. Наприклад при ![]() одержимо
одержимо
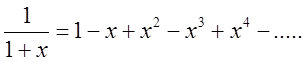 (2.26)
(2.26)
Це випливає з (2.25), хоча його можна дістати й беспосередньо як суму відповідної прогресії.
Якщо замінимо в (2.26) х на –х, то одержимо
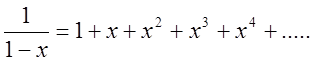 (2.27)
(2.27)
Якщо в (2.26 ) зробимо підстановку ![]() ,
то
,
то
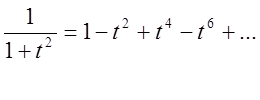 (2.28)
(2.28)
Інтегруючи (2.26) і (2,27) в межах від 0 до х одержимо.
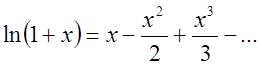 і
і 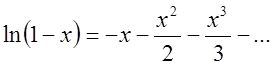 (2.29)
(2.29)
Обидва ці ряди збігаються при ![]() .
.
Розглянемо біноміальний ряд при 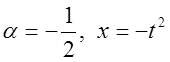 , тобто запишемо розвинення в ряд функції
, тобто запишемо розвинення в ряд функції 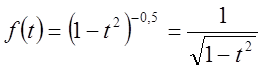 , а потім рівність проінтегруємо в межах
від 0 до t, де
, а потім рівність проінтегруємо в межах
від 0 до t, де ![]() і
одержимо розвинення в степеневий ряд функції
і
одержимо розвинення в степеневий ряд функції ![]() .
.
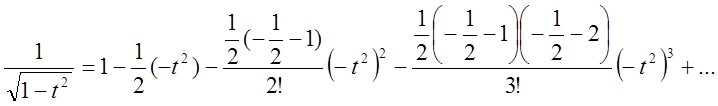
Після очевидних спрощень одержимо
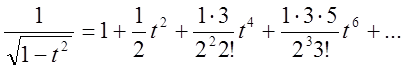 .Проінтегрувавши матимемо
.Проінтегрувавши матимемо
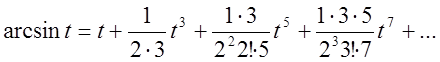 (2.30)
(2.30)
Якщо в (2.26) замість х підставимо ![]() і проінтегруємо одержану рівність то
одержимо
і проінтегруємо одержану рівність то
одержимо
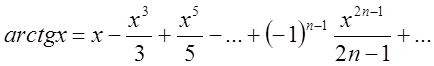 (2.30а)
(2.30а)
П.4. Обчислити суму ряду 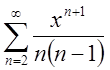
Розв. Питання про збіжність цього ряду вирішується за
допомогою ознаки Даламбера і![]() . Виносячи х за дужки,
одержимо добуток
. Виносячи х за дужки,
одержимо добуток 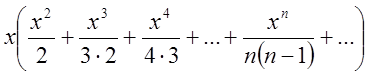 . Присутність однакових чисел в
знаменнику дробів і в показнику степеня чисельника штовхоє нас на думку, що
похідна від ряду, що стоїть в дужках, буде простішою ніж сам ряд. Позначимо
. Присутність однакових чисел в
знаменнику дробів і в показнику степеня чисельника штовхоє нас на думку, що
похідна від ряду, що стоїть в дужках, буде простішою ніж сам ряд. Позначимо 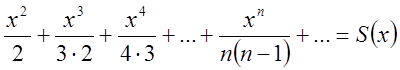 (*) , тоді взявши похідну від обох частин
цієї рівності одеримо
(*) , тоді взявши похідну від обох частин
цієї рівності одеримо 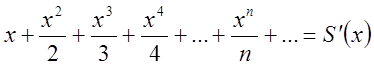 (**). Очевидно, що
коли візьмемо ще раз похідну від обох частин, то ліва частина рівності
перетвориться в звичайну нескінченно спадну геометричну прогресію, суму якої легко
знайти .
(**). Очевидно, що
коли візьмемо ще раз похідну від обох частин, то ліва частина рівності
перетвориться в звичайну нескінченно спадну геометричну прогресію, суму якої легко
знайти .
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.