О. Степеневим рядом називають ряд 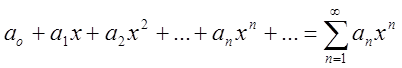 (2. 17)
(2. 17)
Ряд (2.17) називають рядом за степенями х. Тут ![]()
О. Степеневим також називають ряд 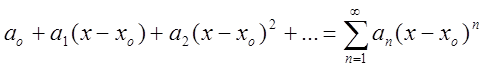 (2. 18)
(2. 18)
Ряди (2.18) називають рядом за степенями ![]() . Тут також
. Тут також ![]() .
.
Виконавши в (2.18) заміну ![]() дістанемо
(2.17). Оскільки ряд (2.17) зручніший за формою, ніж ряд (2.18), то коли це
можливо, користуватимемося рядом (2.17). Степеневий ряд, очевидно, є окремим
випадком функціонального ряду.
дістанемо
(2.17). Оскільки ряд (2.17) зручніший за формою, ніж ряд (2.18), то коли це
можливо, користуватимемося рядом (2.17). Степеневий ряд, очевидно, є окремим
випадком функціонального ряду.
Питання збіжності ряду (2.17) вирішується теоремою Абеля.
Т.а) Якщо степеневий ряд (2.17) збіжний при
![]() то він абсолютно збіжний і при
то він абсолютно збіжний і при ![]() таких, що
таких, що ![]()
б) Якщо степенний ряд (2.17) розбіжний при ![]() , то він розжбіжний і при
, то він розжбіжний і при ![]() таких, що
таких, що ![]() .
.
Дов-ня. а) оскільки ряд ![]() збіжний
при
збіжний
при ![]() , то збіжним є числовий ряд
, то збіжним є числовий ряд ![]() . Звідси
. Звідси ![]() (це є
необхідна умова збіжності) і існує таке
(це є
необхідна умова збіжності) і існує таке ![]() , що
, що
![]() для всіх
для всіх ![]() .
.
Тут скористалися обмеженістю послідовності, яка має границю.
Запишемо таку рівність: 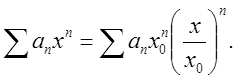 (2.19)
(2.19)
Тоді для членів останнього
ряду матимемо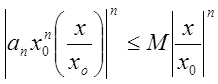 Ряд
Ряд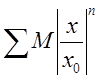
збігається як сума геометричної прогресії зі знамеником 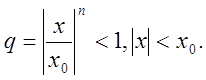 Беручи до уваги те, що
Беручи до уваги те, що 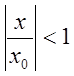 і рівність (2.19), дістаємо доводжуване
твердження теореми.
і рівність (2.19), дістаємо доводжуване
твердження теореми.
|
|
Ураховуючи теорему Абеля, структуру області збіжності (2.17)
можна зобразити так, як показано на рис. 1.1. Перебираючи значення ![]() між
між ![]() і
і ![]() , зближуючи
, зближуючи ![]() і
і ![]() , маємо випадок:
, маємо випадок:
Рис.1.1. існує таке число ![]() , що ряд збіжний при
, що ряд збіжний при ![]() і розбіжним при
і розбіжним при ![]() .
Це число R називають радіусом збіжності ряду, а з
самого визначення радіуса збіжності маємо інтервал збіжності
.
Це число R називають радіусом збіжності ряду, а з
самого визначення радіуса збіжності маємо інтервал збіжності ![]() .
.
Для того щоб знайти радіус збіжності, або зразу інтервал збіжності, застосовують вивчені раніше (лекція 1) достатні умови збіжності числових рядів:
Даламбера 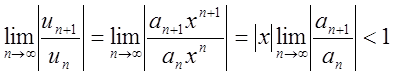
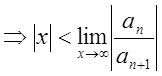 ,
тобто
,
тобто 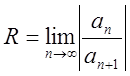 .
.
Радикальний Коші 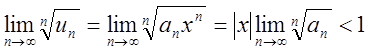 , тобто
, тобто ![]() .
.
Як відомо, і ознака Даламбера і ознака Коші вирішують питання про збіжність (розбіжність) у випадку строгих нерівностей < (>), у випадку = питання про збіжність ряду залишається відкритим. Тому, щоб з’ясувати питання про збіжність ряду на кінцях інтервалу збіжності, тобто при x = –R i x = R, ці значення підставляють в функціональний ряд і досліджують на збіжність числові ряди.
П.3. Знайти інтервал збіжності ряду 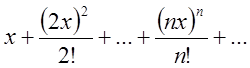 .
.
Роз-ня. D: 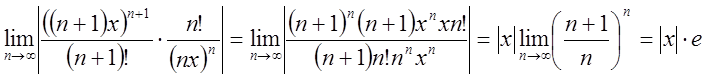 .
.
Далі 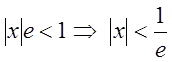 , або
, або 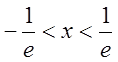 . Дослідимо збіжність на кінцях інтервалу.
. Дослідимо збіжність на кінцях інтервалу.
При 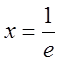 маємо числовий ряд
маємо числовий ряд 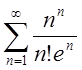 . Перевіримо, чи виконується для нього
необхідна ознака збіжності, тобто чи
. Перевіримо, чи виконується для нього
необхідна ознака збіжності, тобто чи ![]() . Для цього застосуємо
формулу Стерлінга
. Для цього застосуємо
формулу Стерлінга 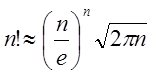 , яка застосовується для великих n.
, яка застосовується для великих n. 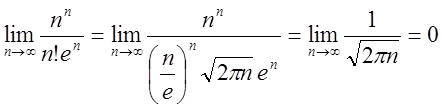
Ознака виконується , ряд може збігатись. За ознакою
Даламбера маємо 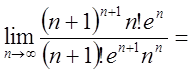
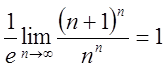 і ми
нічого не можемо сказати про збіжність ряду, тобто ознака Даламбера для цього
ряду не працює. Ознака Коші теж (перевірте).
і ми
нічого не можемо сказати про збіжність ряду, тобто ознака Даламбера для цього
ряду не працює. Ознака Коші теж (перевірте).
При 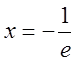 маємо знакопереміжний
числовий ряд
маємо знакопереміжний
числовий ряд 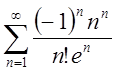 . Перевіримо, чи виконуються для
нього умови теореми Лейбніца. Перша умова
. Перевіримо, чи виконуються для
нього умови теореми Лейбніца. Перша умова 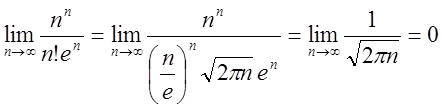
Виконується. Друга 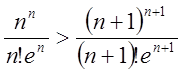 після
скорочень має вид
після
скорочень має вид 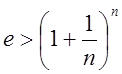 . Послідовність зправа прямує до
е , залишаючись весь час < e, а тому друга умова
також виконана і при
. Послідовність зправа прямує до
е , залишаючись весь час < e, а тому друга умова
також виконана і при 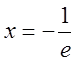 ряд збігається. Відповідь:
ряд збігається. Відповідь: 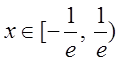 .
.
2.4. Ряди Тейлора і Маклорена
Нехай ![]() де
де ![]() - невідомі коефіцієнти.
- невідомі коефіцієнти.
Знайдемо похідні: ![]()
![]()
![]()
………………………………………………
Якщо ![]() і всі її похідні
визначені в точці
і всі її похідні
визначені в точці ![]() , то, беручи
, то, беручи ![]() , дістаємо
, дістаємо
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.