Функції багатьох змінних. Основні поняття. Межа, безперервність

Лекція 1

План.

1.  Основні поняття. Межа, безперервність.

1. Основні поняття. Межа, безперервність

Нехай дані дві непорожніх безлічі D і U. Якщо кожній парі дійсних чисел , що належить безлічі D, за визначеним правилом ставиться у відповідність один і тільки один елемент і з U, то говорять, що на безлічі D задана функція f (або відображення) з безліччю значень U.

При цьому пишуть , або . Безліч D називається областю визначення функції, а безліч U, що складається з усіх чисел виду , де  – безліччю значень функції. Значення функції  в крапці  позначають  або .

Область визначення функції  в найпростіших випадках являє собою або частину площини, обмежену замкнутою кривою, причому крапки цієї кривої (границі області) можуть належати або не належати області визначення, або всю площину, або, нарешті, сукупність декількох частин площини хОу. Геометричним зображенням функції  в прямокутній системі координат Охуи (графіком функції) є деяка поверхня.

Аналогічно визначається функція будь-якого числа перемінних .

Лінією рівня функції  називається лінія  на площині , у крапках якої функція зберігає постійне значення i=С.

Поверхнею рівня функції  називається поверхня , у крапках якої функція зберігає постійне значення .

Приклад 1.

Знайти область визначення функції .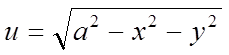

Рішення. Функція u приймає дійсні значення за умови , або , тобто областю визначення даної функції є коло радіуса а з центром на початку координат, включаючи граничну окружність.

Приклад 2.

Знайти лінії рівня функції .

Рішення. Рівняння сімейства ліній рівня має вигляд . Додаючи С різні дійсні значення, одержимо концентричні окружності з центром на початку координат.

Приклад 3.

Знайти поверхні рівня функції .

Рішення. Рівняння сімейства поверхонь рівня має вигляд . Якщо , то одержуємо  – конус; якщо , те  – сімейство однопорожнинних гіперболоїдів; якщо , те  – сімейство двопорожнинних гіперболоїдів.