Числові ряди. Означення ряду та його збіжності. Залишок ряду. Лінійні операції. Знакозмінні ряди. Числоподібні ряди

Лекція №1 

числові Ряди

План:

1.1. Означення ряду та його збіжності.

1.2. Залишок ряду. Лінійні операції.

1.3. Необхідна ознака збіжності.

        1.4. Достатні ознаки збіжності знакододатніх рядів.

1.5. Знакозмінні ряди.

        1.6. Чмслоподібні ряди.

        1.7. Наближене обчислення скми ряду. Прискорення збіжності ряду.

        1.8. Запитання для самоперевірки.

Українсько-російський словник вжитих в лекції слів, які в мовах мають різне звучання.

Математичні факти з попередніх розділів, які використовуються в даній лекції.

1.Послідовністьвважається заданою, якщо задано відповідний закон за яким для кожного натурального  можна поставити у відповідність деякий вираз .

Коротко кажучи, числова послідовність є функція від натурального аргумента. Якщо розписати числову послідовність , то кожне значення із цієї послідовності залежить по загальній для всього набору формулі від номера свого місця в цьому наборі. Наприклад.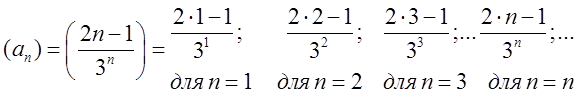

Чисельники цієї послідовності утворюють арифметичну прогресію, а знаменники – геометричну. Нас буде цікавити формула суми нескінченно спадної геометричної прогресії 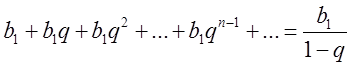. Арифметична прогресія нас не цікавить з тієї причини, що сума нескінченниго числа її членів завжди дорівнює .

2. Пригадаймо деякі факти з теорії границь: перша стандартна границя 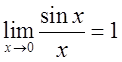  і  одержаний звідси набір еквівалентних величин ; друга стандартна границя 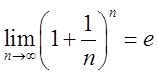. При обчисленні границь від дробових виразів одержуємо 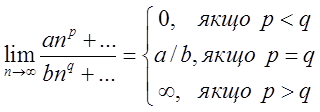 тут р найбільший показник чисельника, а q  найбільший показник знаменника, причому . Слід також пам’ятати, що  (при а>1) причому, тут символ < вживається в контексті того, що границя відношення попереднього виразу до кожного з наступних дорівнює нулеві, так паприклад .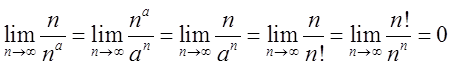

3. Іноді корисно застосувати асимптотичну формулу Стерлінга .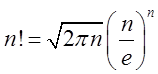

4.Пригадаймо обчислення невластивих інтегралів

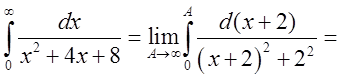
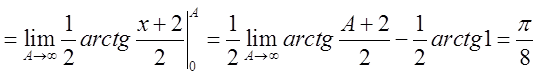. Цей інтеграл має суму тому він збіжний, а якщо невластивий інтеграл не має суми, то він розбіжний.

Деякі попередні зауваження.

Проблеми переходу скінченного в нескінченне і навпаки, подільності на нескінченно малі елементи простору і часу цікавили людство з глибокої древності. Саме диференціальне та інтегральне числення є числення нескінченно малих величин і відкрили його не менш великі філософи ніж математики. З появою цього числення були розв’язані не лише чисто практичні математичні задачі, а й задачі філософські,  які віками штовхали мислителів на невірні колії пошуку істини. Розглянемо і ми одну з них, це так званий апорій Зенона. В часи Зенона (Древня Греція 5-4 в д.н.е) між філософами розгорівся диспут про нескінченну подільність простору і часу. На припущення що такий поділ можливий Зенон поставив задачу з очевидним розв’язком. На деякій відстані (нехай 100 м) Ахіл побачив черепаху, вона побачила його, і одночасно він кинувся її наздоганяти, а вона – від нього втікати. Біжать по прямій лінії. Швидкість Ахіла вдвічі  більша ніж у черепахи. Якщо процес поділу до нескінченності простору і часу можливий, то він її ніколи б не наздогнав. Зенон це показує, розглядаючи  процес наздоганяння  так: перш ніж наздогнати черепаху Ахіл повинен прибігти в те місце де вона була на початку наздоганяння; для того, щоб прибігти в це місце йому потрібен час; за цей час черепаха відбіжить від попереднього місця на віддаль вдвічі меншу, ніж попередня  і їх розділяє 50 м. Тепер знову перш ніж наздогнати черепаху Ахіл повинен прибігти в те місце де вона була на другому етапі наздоганяння; для того, щоб прибігти в це місце йому потрібен час; за цей час черепаха відбіжить від попереднього місця на віддаль вдвічі меншу, ніж попередня. Тепер їх розділяє 25 м. І так розмірковуючи, завдяки припущенню, що час і простір можна ділити до нескінченності, ми прийдемо до того, що Ахіл ніколи не зможе її наздогнати. Однак він же її наздоганяє. Звідси висновок про помилковість припущення про нескінченну подільність простору і часу. В крайньому разі одне з них має дискретну будову. Так міркували древні. Ми з Вами запишемо суму тих послідовних відрізків віддалей, які пробіг Ахіл до моменту наздогнання черепахи. 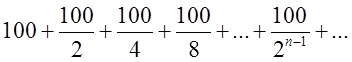Їх і справді буде нескінченно багато .Для черепахи одержимо таку ж суму, але в чисельнику буде замість 100 скрізь 50. Зрозуміло, що кожна із сум має якесь визначене значення (насправді він же її наздоганяє).       

Розглянемо інший вираз: суму