 .
.
Для збіжного ряду (1.2) маємо 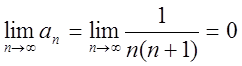 .
.
1.4. Достатні ознаки збіжності знакододатних рядів
Нижче розглядатимемо тільки знакододатні ряди (1.1), тобто ряди, в яких
![]() . Згідно з теоремою 2, 1.2, немає
необхідності окремо розглядати випадки знаковід’ємних рядів.
. Згідно з теоремою 2, 1.2, немає
необхідності окремо розглядати випадки знаковід’ємних рядів.
Нагадаємо один результат з теорії границь: монотонно зростаюча й обмежена зверху послідовність має границю. Тепер переходимо до ознак збіжності рядів.
Ознаки порівняння (О – П)
Т.1. Нехай маємо ряди![]() , (*)
, (*) ![]() , (**)
, (**)
причому ![]() . Тоді із збіжності ряду (**) випливає збіжність ряду (*), а з розбіжності ряду (*)
випливає розбіжність ряду (**).
. Тоді із збіжності ряду (**) випливає збіжність ряду (*), а з розбіжності ряду (*)
випливає розбіжність ряду (**).
Доведемо перше твердження. Нехай
![]() ,
, ![]() .
.
За умовою теореми ![]() . Отже,
. Отже, ![]() ,
,
тобто послідовність
![]() обмежена зверху числом
обмежена зверху числом ![]() і є очевидно зростаючою (всі члени ряду додатні). Тоді існує границя
послідовності
і є очевидно зростаючою (всі члени ряду додатні). Тоді існує границя
послідовності ![]() , тобто ряд (1) – збіжний. Доведення
другого твердження аналогічне.
, тобто ряд (1) – збіжний. Доведення
другого твердження аналогічне.
На практиці зручніше користуватись граничною ознакою порівняння, яку виражає Т.2. і яку ми подаємо без доведення (доведення можна знайти в [2])
Т.2. Нехай маємо ряди ![]() , (*)
, (*) ![]() , (**)
, (**)
Якщо  то ряд (*) і ряд (**) мають
однакову поведінку тобто вони одночасно розбігаються, або одночасно збігаються.
то ряд (*) і ряд (**) мають
однакову поведінку тобто вони одночасно розбігаються, або одночасно збігаються.
П. 1. Дослідити на збіжність ряд 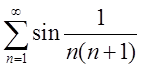 .
.
Розв’язання. Маємо 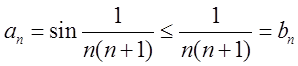 ,
,
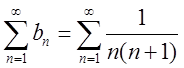 .
.
Останній ряд збіжний див П.1, а тому за теоремою порівняння (Т-1) досліджуваний ряд збігається.
Ознака д’Аламбера (О –Д)
Т. Якщо![]() -загальний член ряду і
-загальний член ряду і 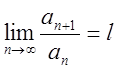 (1.6)
(1.6)
То а) при ![]() ряд збіжний, б) при
ряд збіжний, б) при ![]() ряд розбіжний,
ряд розбіжний,
в) при ![]() ознака не чинна: існують ряди
збіжні, для яких
ознака не чинна: існують ряди
збіжні, для яких ![]() і розбіжні, для яких теж
і розбіжні, для яких теж ![]() .
.
а) Застосуємо означення границі до ряду (1.6). Тоді для довільного ![]() існує такий номер
існує такий номер ![]() ,
що при
,
що при ![]()
 .
(1.7)
.
(1.7)
Візьмемо таке довільне ![]() , що
, що ![]() . Нехай в нерівності (1.7)
. Нехай в нерівності (1.7) ![]() , тоді при
, тоді при ![]()
![]() . Реалізуємо останню нерівність при
. Реалізуємо останню нерівність при ![]() ,
, ![]() і т. д.
і т. д.
Дістаємо ![]() ,
, ![]() , …
, …
Розглянемо ряди ![]() ,
, ![]() .
.
Другий ряд збіжний
як сума геометричної прогресії (1.3), в якій ![]() . Перший
ряд збіжний згідно з ознакою порівняння, але перший ряд – це залишок вихідного
ряду після члена
. Перший
ряд збіжний згідно з ознакою порівняння, але перший ряд – це залишок вихідного
ряду після члена ![]() . Беручи до уваги ознаку
порівняння рядів, дійдемо висновку, що заданий ряд теж збіжний. Нескладне
доведення пункту б) проведіть самостійно.
. Беручи до уваги ознаку
порівняння рядів, дійдемо висновку, що заданий ряд теж збіжний. Нескладне
доведення пункту б) проведіть самостійно.
в) Для ряду (1.2) і
для гармонічного ряду маємо  .
.
Проте перший – збіжний, а другий – розбіжний.
П. 3. Дослідити на збіжність 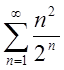 . Застосуємо ознаку д’Аламбера, маємо
. Застосуємо ознаку д’Аламбера, маємо
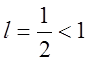 , Отже, ряд збіжний.
, Отже, ряд збіжний.
Для дослідження на збіжність рядів у яких n знаходиться в показнику степеня найзручнішою є радикальна ознака Коші, яку ми подамо без доведення.
Радикальна ознака Коші (Р – К)
Т. Якщо![]() – загальний член ряду і
– загальний член ряду і ![]() (1.8)
(1.8)
то а) при ![]() ряд збіжний, б) при
ряд збіжний, б) при ![]() ряд розбіжний,
ряд розбіжний,
в) при ![]() ознака не чинна: існують ряди
збіжні, для яких
ознака не чинна: існують ряди
збіжні, для яких ![]() і розбіжні, для яких теж
і розбіжні, для яких теж ![]() .
.
Інтегральна ознака Коші-Маклорена (І – К)
Т. 3. Якщо члени ряду (1.1) утворюють незростаючу послідовність ![]() й
існує незростаюча неперервна невід’ємна функція
й
існує незростаюча неперервна невід’ємна функція ![]() така,
що
така,
що
![]() ,
, ![]() ,…,
,…, ![]() ,…,
,…,
то ряд (1.1) і невластивий інтеграл 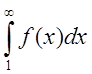 (1.9)
(1.9)
збігаються або розбігаються одночасно.
Для доведення цієї
ознаки замінимо ![]() кусково-сталою, як показано на
рис. 2.1.
кусково-сталою, як показано на
рис. 2.1.
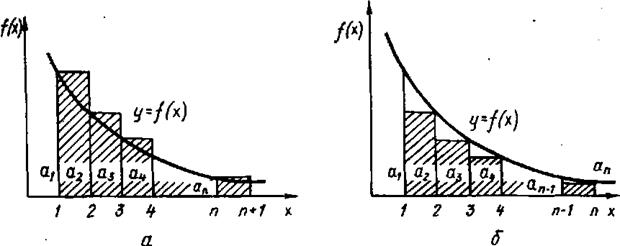
рис. 2. 1.
Дістанемо ступінчасті фігури, з яких площа однієї не менша (рис. 2.1,
а), а другої – не більша, ніж площі відповідних криволінійних трапецій. Для ![]() (рис. 2.1,а) і для
(рис. 2.1,а) і для ![]() (рис.
2.1, б) маємо
(рис.
2.1, б) маємо ![]()
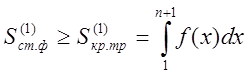 ,
,
Тобто 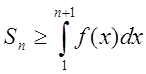 ,
, 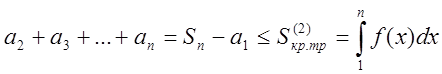 ,
,
Тобто 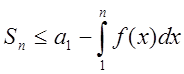 . З двох оцінок для
. З двох оцінок для ![]() дістаємо
дістаємо
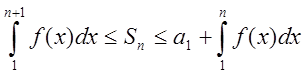 .
(1.10)
.
(1.10)
Нехай ряд (1.9) –
збіжний. Тоді 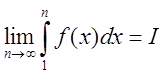 . З нерівності (1.10) маємо
. З нерівності (1.10) маємо ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.