Числові ряди. Означення ряду та його збіжності. Залишок ряду. Лінійні операції. Знакозмінні ряди. Числоподібні ряди, страница 2

Вважатимемо, що для такої нескінченної суми виконується асоціативний закон додавання. Тоді суму S розумітимемо як   ,   або

.

Припустимо, що з нескінченної суми можна винести спільний множник.

Тоді    .

Отже, для одного і того самого виразу дістали три різні значення. Проте операція додавання однозначна. Звідси випливає, що для нескінченних сум і асоціативний закон, і властивість однорідності або не справджуються, або виконуються з певними обмеженнями. Згадаємо, що властивості адитивності для границі, похідної, інтеграла ми формулювали лише для скінченого числа функцій.

Таким чином, властивості скінчених сум можуть істотно відрізнятись від властивостей нескінченних сум. Частково з огляду на це ми переходимо до вивчення таких сум.

1.1. Означення ряду та його збіжності

Нехай маємо послідовність , для елементів якої виконується операція додавання.

           О. Рядом, складеним з елементів послідовності , називається символ

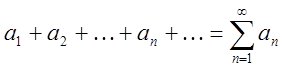,                                                   (1.1)

який розуміють спеціальним чином.

У запису (1.1) а_n називають загальним або n-м членом.

Утворимо так звані часткові суми (1.1)

,

,

.........................

і розглянемо послідовність їх .

О. Ряд називається збіжним, якщо існує скінчена границя послідовності його частинних сум,       .

О. Ряд називається розбіжним, якщо границя послідовності його частинних сум або нескінченна, або не існує.

О. Сумою ряду називається границя послідовності його частинних сум, якщо вона існує, тобто 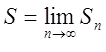      .     Отже, S може бути скінченим числом або нескінченністю.

            П. 1. Дослідити на збіжність ряд

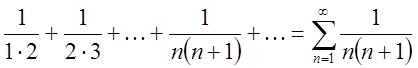.                              (1.2)

Р о з в ‘ я з а н н я. Маємо    ,    ,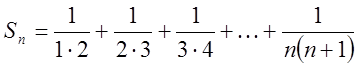

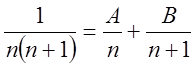звідки . Так, як ця рівність повинна виконуватись тотожньо відносно п (для всіх значень ), то надаючи значення , одержимо систему з якої і знайдемо А, В. Маємо А = 1, В = -1. Отже, остаточно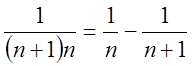. Застосувавши цей результат до кожного доданка, дістанемо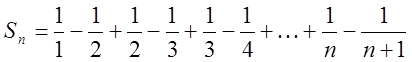,  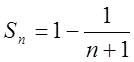    ,    звідки 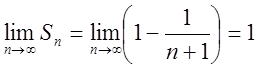.Отже, ряд (1.2) збіжний, S = 1.

          П. 2. Дослідити на збіжність геометричний ряд, тобто суму нескінченної геометричної прогресії ()   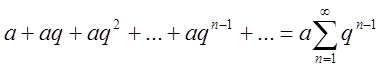 .                                                        (1.3)

Як відомо,   , .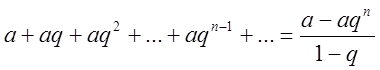

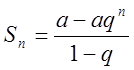Розглянемо такі випадки

I випадок. Нехай . Тоді 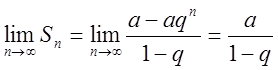  . Отже, ряд збіжний, .

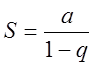II випадок. Нехай . Тоді 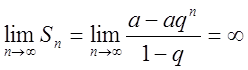  .  Отже, ряд розбіжний, .

III випадок. Нехай . Тоді   ,    .

Отже, ряд розбіжний, .

IV випадок. Нехай . Тоді    ,

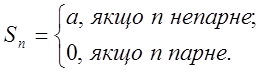
Оскільки , то послідовність  коливається і границі не має. Ряд розбіжний. Отже, ряд (1.3) збіжний при  і розбіжний при .

1.2. Залишок ряду. Лінійні операції

Розглянемо ряд     .

О. Залишком ряду після -го члена називають ряд   ,

Тобто   .

Замість “залишок ряду після -го члена” кажуть іноді “залишок ряду”.

Т. 1. Ряд і його залишок або одночасно збігаються, або одночасно розбігаються.

У виразі        позначимо , . Тоді   , .

 Звідси випливає твердження теореми.

Розглянемо лінійні операції над рядами.

Т. 2. Нехай маємо  ,                                                                            (1.4)

                                 .                                                                            (1.5)

Тоді         Якщо (1.4) збігається, то  ряд  

теж збігається і           ;

1)  Якщо ряди (1.4) і (1.5) збігаються, то ряд  

теж збігається і    .

Доведення теореми є модифікацією відповідних теорем про границю послідовності.

1.3. Необхідна ознака збіжності (НОЗ)

Розглянемо ознаки, за допомогою яких можна встановити факт збіжності чи розбіжності ряду. Необхідну ознаку збіжності дає така теорема.

Т. Якщо ряд збігається, то послідовність його членів прямує до нуля, тобто якщо ряд (1.1) збігається, то   .

Справді, збіжність ряду (1.1) означає, що , де

,  тобто   ,   звідки

.

Доведена ознака є необхідною, але не є достатньою. Зазначимо, що гармонічний ряд, тобто ряд     є розбіжним (цей факт доведемо пізніше), хоча