Числові ряди. Означення ряду та його збіжності. Залишок ряду. Лінійні операції. Знакозмінні ряди. Числоподібні ряди, страница 4

Тобто послідовність  зростає і обмежена зверху (числом ).

Тому,  , заданий ряд збіжний. Коли інтеграл (1.9) збіжний, то    .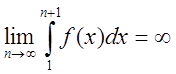

Використовуючи ліву частину нерівності (1.10), маємо, що   , тобто ряд

розбіжний. Решта тверджень теореми доводиться аналогічно.

Зауваження

1.Теорема 3 справджується, якщо послідовність  задовольняє умови теореми, починаючи хоча б з деякого номера (тоді користуємося теоремою 1, п. 1.1.2).

Те саме стосується й нерівності  в теоремі 1 цього пункту.

2.Якщо ряд збіжний, то, перейшовши до границі в (1.10), дістанемо оцінку

.

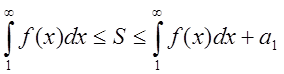            П.4. За допомогою інтегральної ознаки дослідити на збіжність узагальнений гармонічний ряд

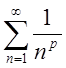                                          , .                                                                                                                                                                               (1.11)

Розв’язання. Маємо 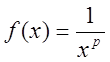 . Функція  задовольняє умови теореми 3. Розглянемо інтеграл 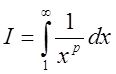 .    При    .

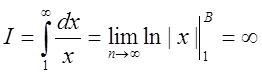Інтеграл і заданий ряд (до речі, гармонічний) розбіжні.

Нехай . Тоді  .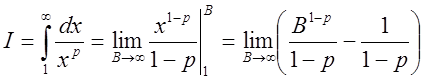

Якщо , то 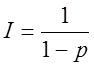; якщо , то .

Остаточно дістаємо: ряд (1.11) розбігається при  і збігається при .

1.5. Знакозмінні ряди

Знакозмінними є такі ряди, що містять нескінченну множину як додатних, так і від’ємних членів.

Розглянемо спочатку окремий випадок знакозмінних рядів – знакопереміжні ряди.

О. Знакопереміжним називається ряд

,    для всіх .                                 (1.12)

Ознаку збіжності таких рядів містить наступна теорема.

Т. (Лейбніца). Якщо послідовність членів ряду (1.12)

1)  є спадною (),

2)  такою, що , то

а)  ряд (1.12) збігається,

б)  якщо  - сума ряду (1.12), то .

Розглянемо послідовність частинних сум (1.12) з парними номерами. Маємо

,

оскільки кожна дужка додатна; запишемо  у вигляді

.

Звідси , оскільки кожна дужка знову-таки додатна.

Беручи до уваги, те, що послідовність  зростаюча й обмежена, дістаємо

.

Для сум з непарними номерами маємо

.  Отже,    ,

тобто (1.12) збігається, крім того, .

Зауваження. Теорема Лейбніца справджується, якщо послідовність членів (1.12) є спадною хоча б з деякого номера.

Наслідок. Оскільки залишок (1.12)  є в свою чергу знакопереміжним рядом, то

,    .

П. 5. Обчислити з точністю до 0.1 суму ряду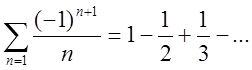в разі його збіжності.

Розв’язання. Згідно з теоремою Лейбніца, заданий ряд збігається,  .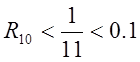

Тоді за наслідком з теореми Лейбніца

.

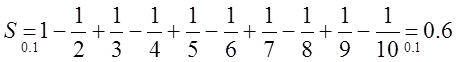Порівняйте цей ряд з гармонічним, який є розбіжним.

Перейдемо до ознак збіжності знакозмінних рядів.

Т. Із збіжності ряду 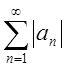 випливає збіжність знакозмінного ряду .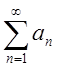

Зауваження. Обернене твердження в загальному випадку не виконується (див. П. 1.).

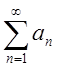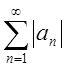О. Якщо для знакозмінного ряду  ряд  збігається, то знакозмінний ряд називають абсолютно збіжним.

О. Якщо знакозмінний ряд 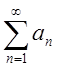 збіжний, а ряд  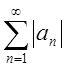розбіжний, то знакозмінний ряд називають умовно збіжним.

П. 6. Ряд у попередньому прикладі умовно збіжний, а ряд

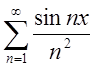               абсолютно збіжний, бо            .

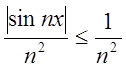Зазначимо, що в абсолютно збіжному ряді члени можна переставляти як завгодно, це не впливає на суму, а в умовно збіжному ряді для довільного числа  можна знайти таку перестановку членів ряду, що сума його , навіть (теорема Рімана).

Це твердження свого часу поставило під сумнів застосування рядів для наближених обчислень, проте це не так, треба тільки розрізняти абсолютну й умовну збіжність рядів і враховувати властивості їх.

1.6. Числоподібіні ряди

До числоподібних рядів належать ряди з комплексними, векторними, тензорними (матричними) членами.

Ряд з комплексними членами – це ряд     .

Відокремлюючи дійсну й уявну частини ряду, дістаємо два ряди

,      .

Якщо кожен з них збіжний, то збіжний і ряд по . Якщо хоч один з них розбіжний, то ряд по  розбіжний. Якщо збігається ряд з модулів , то ряд по  називають абсолютно збіжним.

Ряд з векторними членами має вигляд   ,