Числовий ряд, часткові суми ряду. Збіжність і сума ряду. Необхідна умова збіжності

Лекція 1

План.

1.  Числовий ряд, часткові суми ряду. Збіжність і сума ряду.

2.   Необхідна умова збіжності.

1. Числовий ряд, часткові суми ряду. Збіжність і сума ряду

Визначення 1. Нехай задана нескінченна послідовність чисел

.

Вираження

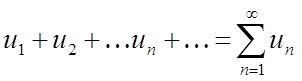                            (1)

називається числовим рядом.

При цьому числа  називаються членами ряду,  – загальний член ряду.

Визначення 2. Сума кінцевого числа n перших членів ряду називається n-й частковою сумою ряду.

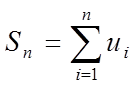.                                        (2)

Визначення 3. Якщо існує кінцева межа 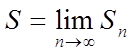, то її називають сумою ряду (1) і говорять, що ряд збігається.

Якщо 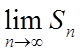 не існує (наприклад,  при ), то говорять, що ряд (1) розбігається і суми не має.

Наприклад: розглянемо убутну геометричну прогресію зі знаменником :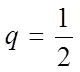

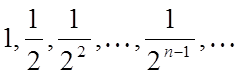
Складемо ряд із членів цієї прогресії

.

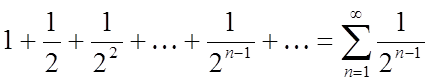Сума n перших членів геометричної прогресії :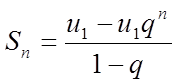

.

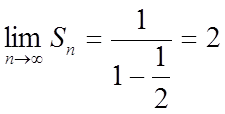По визначенню 3:

Властивості рядів, що збігаються

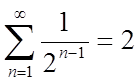
1.  При додаванні або вирахуванні рядів, що збігаються, одержуємо ряд, що збігається.

2.  При множенні ряду, що збігається, на постійний множник одержуємо ряд, що збігається.

3.  На збіжність ряду не впливає відкидання кінцевого числа його членів.

2. Необхідна ознака збіжності ряду

Теорема. Якщо ряд збігається, то його n-й член прагне до нуля при .

Доказ.

Тому що ряд збігається, то 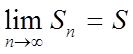, де S – сума ряду, але тоді і 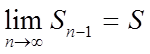, тому що при  і . Знайдемо різницю меж:

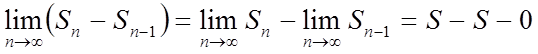, але ; тобто 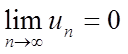, що і було потрібно довести.

Наприклад:

;           .

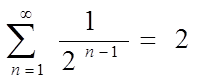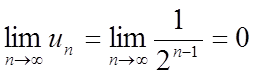Наслідок. Якщо n-й член ряду не прагне до нуля при , то ряд розбігається.