Комплект контрольних завдань з дисципліни "Випадкові процеси"

Практична частина

Двовимірний  закон  розподілу  випадкової   величини  записується

щільністю:

.

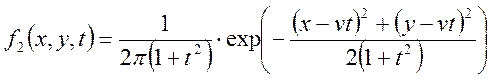Знайти всі ймовірні характеристики.

                         Завідувач кафедри ........................................................ проф.Грибанов В.М.

                                                                                                           (підпис)

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ СХІДНОУКРАЇНСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ

ім. В. Даля

Кафедра прикладної математики

Спеціальність 80202 - прикладна математика

КОНТРОЛЬНЕ   ЗАВДАННЯ    02

з дисципліни «Випадкові процеси»

Теоретична частина

1.  Основні поняття і співвідношення в задачі аналізу тимчасових рядів.

2.  Спектральне представлення лінійних операцій. Лінійний фільтр.

Практична частина

Вв є часткою случаємо такої випадкової функції, у якого відсутня     залежність від часу : й описується показовим законом розподілу, з     ().

Знайти: , , .

                              Завідувач кафедри ........................................................ проф.Грибанов В.М.

                                                                                                             (підпис)

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ СХІДНОУКРАЇНСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ

ім. В. Даля

Кафедра прикладної математики Спеціальність 80202 - прикладна математика

КОНТРОЛЬНЕ   ЗАВДАННЯ    03

з дисципліни «Випадкові процеси»

Теоретична частина

1.  Критерії випадковості. Екстремальні крапки.

2.  Зргодичний стаціонарний в.п.

Практична частина

Випадковий процес має вид , . — вв, рівномірно розподілена на відрізку . Знайти одномірну функцію і щільність розподілу.

                              Завідувач кафедри ........................................................ проф.Грибанов В.М.

                                                                                                             (підпис)

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ СХІДНОУКРАЇНСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ

ім. В. Даля

Кафедра прикладної математики Спеціальність 80202 - прикладна математика

КОНТРОЛЬНЕ   ЗАВДАННЯ    04

з дисципліни «Випадкові процеси»

Теоретична частина

0.  Закон розподілу в.п. Ймовірні характеристики в.п.

1.  Нормальні в.п.

Практична частина

Вв задана у виді .  — вв, що підкоряється нормальному закону з параметрами , .   — невипадкова   константа.   Знайти   одномірну   щільність

 і , , .

                              Завідувач кафедри ........................................................ проф.Грибанов В.М.

                                                                                                             (підпис)

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ СХІДНОУКРАЇНСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ

ім. В. Даля

Кафедра прикладної математики Спеціальність 80202 - прикладна математика

КОНТРОЛЬНЕ   ЗАВДАННЯ    05

з дисципліни «Випадкові процеси»

Теоретична частина

1. Закони розподілу й осередненні характеристики випадкових функцій

(с.ф.).

2. Корелограма.

Практична частина

Випадкова функція  , де  і  —незалежні вв, що підкоряються тому самому нормальному закону розподілу .

Використовуючи властивості математичного чекання і дисперсії обчислити , ,  й одномірну щільність .