Комплект контрольних завдань з дисципліни "Випадкові процеси", страница 4

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ СХІДНОУКРАЇНСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ

ім. В. Даля

Кафедра прикладної математики Спеціальність 80202 - прикладна математика

КОНТРОЛЬНЕ   ЗАВДАННЯ    17

з дисципліни «Випадкові процеси»

Теоретична частина

1.  Періодичні стаціонарні процеси.

2.  Аналіз тренда. Сезонні коливання.

Практична частина

Узагальнений телеграфний сигнал .

Імовірність зміни знака на інтервалі  не залежить від того, що відбувалося поза цим інтервалом. Імовірність того, що протягом Інтервалу тривалістю  відбудеться змін знака випадкової величини :

, ,

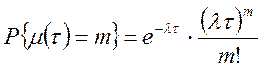 — середнє число змін значень випадкового процесу в одиницю часу. Знайти ймовірні характеристики узагальненого телеграфного сигналу й установити безперервність телеграфного сигналу.

                   Завідувач кафедри ........................................................ проф.Грибанов В.М.

                                                                                                         (підпис)

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ СХІДНОУКРАЇНСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ

ім. В. Даля

Кафедра прикладної математики Спеціальність 80202 - прикладна математика

КОНТРОЛЬНЕ   ЗАВДАННЯ    18

з дисципліни «Випадкові процеси»

Теоретична частина

1. Стаціонарні тимчасові ряди.

2. Процеси з незалежними збільшеннями.

Практична частина

Задано випадковий процес  ;  А   і  —невипадкові

величини; а початкову фазу  — випадкову величину, рівномірно розподілена на інтервалі , тобто щільність розподілу має вид:

.

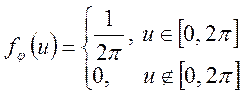Знайти ймовірні характеристики похідної .

                   Завідувач кафедри ........................................................ проф.Грибанов В.М.

                                                                                                         (підпис)

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ СХІДНОУКРАЇНСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ

ім. В. Даля

Кафедра прикладної математики Спеціальність 80202 - прикладна математика

КОНТРОЛЬНЕ   ЗАВДАННЯ    19

з дисципліни «Випадкові процеси»

Теоретична частина

1.  Неперіодичний стаціонарний процес і його спектральне представлення.

2.  Безупинна складова процесу з незалежними збільшеннями.

Практична частина

Послідовність прямокутних імпульсів не дорівнюють одиниці, причому

зміна їхніх значень приходить у випадкові моменти часу, що утворять пуассоновский потік (узагальнений телеграфний сигнал). Показати, що такий процес не диференціюємо.

                   Завідувач кафедри ........................................................ проф.Грибанов В.М.

                                                                                                         (підпис)

МІНІСТЕРСТВО ОСВІТИ  І  НАУКИ  УКРАЇНИ СХІДНОУКРАЇНСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ

ім. В. Даля

Кафедра прикладної математики Спеціальність 80202 - прикладна математика

КОНТРОЛЬНЕ   ЗАВДАННЯ    20

з дисципліни «Випадкові процеси»

Теоретична частина

1.  Властивості спектральної щільності стаціонарного процесу.

2.  Процес броуновского руху.
Практична частина

Чи буде диференціруємим процес .

A і невипадкові величини, а  — випадкова величина з щільністю розподілу: .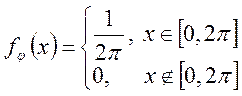

                   Завідувач кафедри ........................................................ проф.Грибанов В.М.

                                                                                                         (підпис)

МІНІСТЕРСТВО ОСВІТИ  І  НАУКИ  УКРАЇНИ СХІДНОУКРАЇНСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ

ім. В. Даля

Кафедра прикладної математики Спеціальність 80202 - прикладна математика

КОНТРОЛЬНЕ   ЗАВДАННЯ    21

з дисципліни «Випадкові процеси»

Теоретична частина

1.  Визначення випадкового процесу (в.п.). Приклади.

2.  Спектральне представлення лінійних операцій. Лінійний фільтр.

Практична частина

Випадковий процес має вид , .  — вв, рівномірно розподілена на відрізку . Знайти одномірну функцію і щільність розподілу.