Комплект контрольних завдань з дисципліни "Випадкові процеси", страница 5

                   Завідувач кафедри ........................................................ проф.Грибанов В.М.

                                                                                                         (підпис)

МІНІСТЕРСТВО ОСВІТИ  І  НАУКИ  УКРАЇНИ СХІДНОУКРАЇНСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ

ім. В. Даля

Кафедра прикладної математики Спеціальність 80202 - прикладна математика

КОНТРОЛЬНЕ   ЗАВДАННЯ    22

з дисципліни «Випадкові процеси»

Теоретична частина

1.  Закон розподілу в.п. Ймовірні характеристики в.п.

2.  Корелограма.

Практична частина

Задано дві щільності  і  двох випадкових незалежних вв  і . Записати одномірну щільність  процесу , .

                   Завідувач кафедри ........................................................ проф.Грибанов В.М.

                                                                                                         (підпис)

МІНІСТЕРСТВО ОСВІТИ  І  НАУКИ  УКРАЇНИ СХІДНОУКРАЇНСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ

ім. В. Даля

Кафедра прикладної математики Спеціальність 80202 - прикладна математика

КОНТРОЛЬНЕ   ЗАВДАННЯ    23

з дисципліни «Випадкові процеси»

Теоретична частина

1.  Кореляційна функція в.п. і її властивості.

2.  Виробляюча функція автокореляцій.

Практична частина

Матеріальна крапка може знаходитися або у вершинах трикутника ABC(мал.1), або переміщатися від однієї вершини до іншої в зазначених на малюнку напрямках з відповідними імовірностями: у т. A— з імовірністю , у т. B — 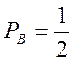;  у т. C — 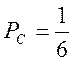; переміщатися від C до Aз імовірністю 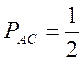, від С до B — 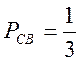, від B до A — .

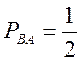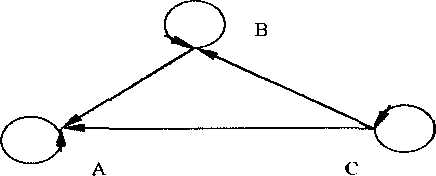
                           Мал .1

Знайти матрицю перехідних імовірностей за два кроки.

                             Завідувач кафедри ........................................................ проф.Грибанов В.М.

                                                                                                             (підпис)

МІНІСТЕРСТВО ОСВІТИ  І  НАУКИ  УКРАЇНИ СХІДНОУКРАЇНСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ

ім. В. Даля

Кафедра прикладної математики Спеціальність 80202 - прикладна математика

КОНТРОЛЬНЕ   ЗАВДАННЯ    24

з дисципліни «Випадкові процеси»

Теоретична частина

1.  Взаємна кореляційна функція і її властивості.

2.  Прогноз і фільтрація стаціонарних процесів.

Практична частина

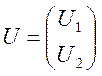Випадковий процес заданий наступним вираженням: , де  — випадковий вектор з вектором математичних чекань 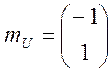 і коваріаціонною матрицею 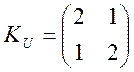; вектор координатних функцій .

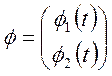Знайти канонічне розкладання процесу і записати автоковариационную функцію.

                             Завідувач кафедри ........................................................ проф.Грибанов В.М.

                                                                                                             (підпис)

МІНІСТЕРСТВО ОСВІТИ  І  НАУКИ  УКРАЇНИ СХІДНОУКРАЇНСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ

ім. В. Даля

Кафедра прикладної математики Спеціальність 80202 - прикладна математика

КОНТРОЛЬНЕ   ЗАВДАННЯ    25

з дисципліни «Випадкові процеси»

Теоретична частина

1.  Вимірні с.ф. Безупинні с.ф.

2.  Негармонійні коливання. Згладжування спектра. Нерівні тимчасові
інтервали.

Практична частина

Випадковий процес , де  — випадкова величина така, що . Знайти ймовірні характеристики випадкового процесу .

                             Завідувач кафедри ........................................................ проф.Грибанов В.М.

                                                                                                             (підпис)

МІНІСТЕРСТВО ОСВІТИ  І  НАУКИ  УКРАЇНИ СХІДНОУКРАЇНСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ

ім. В. Даля

Кафедра прикладної математики Спеціальність 80202 - прикладна математика

КОНТРОЛЬНЕ   ЗАВДАННЯ    26

з дисципліни «Випадкові процеси»

Теоретична частина

1.  Диференціювання стаціонарного в.п.